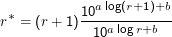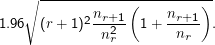Schritt 3: Berechnung der Schätzwerte
Wir können jetzt die Good-Turing-Formeln von oben anwenden. Zunächst ist P0 = n1∕N. Was mit dieser Größe anzufangen ist,
hängt von der Anwendung ab.
Wir rechnen jetzt r* als (r+ 1)nr+1∕nr aus. Mit fallenden nr wird das irgendwann schlechter als als die Schätzungen aus der
linearen Regression. Spätestens wenn ein nr+1 undefiniert ist, schalten wir um auf
mit der
Steigung
a und Achsenabschnitt
b der Regressionsgeraden.
Dieser Ausdruck lässt sich natürlich zu r* = (r+ 1)10a log((r+1)∕r) vereinfachen. Tieferes Nachdenken liefert, dass man schon
Umschalten sollte, wenn die Differenz aus rohen und geglätteten r* größer wird als
Die
Wurzel in diesem magischen Wert ist gerade eine Schätzung für die Varianz von
r (das ja eine Zufallsvariable ist), die 1.96 kommt
daraus, dass die Entscheidung wieder mal zu einem Niveau von 0.05 gefällt werden soll. Es ist offensichtlich, dass man sich an diese
Vorschriften nicht allzu sklavisch halten muss.
Evaluation
Test mit bekannter Ground Truth: Synthese eines Textes auf der Basis eine angenommenen Verteilung von 8743 Wörtern. Plot des
quadratischen Fehlers, zunächst nur für gesehene Wörter:
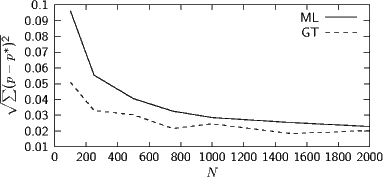
Mit P(w) = P0∕|U| für ungesehene Wörter bei Good-Turing (U ist die Missing Mass):
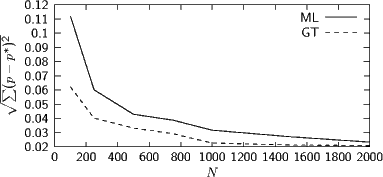
(1)
Besorgt euch die Dateien bigrams.dist, goodturing.py und bigramModels.py von der Webseite zur Vorlesung. Werft einen kurzen Blick
auf goodturing.py, um eine Vorstellung zu bekommen, dass hier tatsächlich ein Good-Turing-Schätzer implementiert
ist.
Nehmt zunächst die Datei bigrams.dist. In ihr stehen in jeder Zeile zunächst zwei Zeichen und dann die Häufigkeit dieser
Zeichenkombination. Prüft zunächst, ob die (hier aus irgendeinem deutschen Korpus gewonnenen) Bigramme von Buchstaben auch
annähernd nach Zipf verteilt sind. Das geht mit der Unix-Shell und gnuplot recht einfach: Mit
cut -b 4- bigrams.dist | sort -n | uniq -c > rnr.dist
bekommt ihr in rnr.dist eine Verteilung von rüber nr (Vorsicht: der Plot wird dann anders orientiert sein als gewohnt, wir haben
bisher immer nr über r aufgetragen). Lest in den manpages zu den Programmen nach, was hier passiert, wenn es euch nicht eh schon
klar ist. Jetzt ruft ihr gnuplot auf und sagt
set logscale xy
plot "rnr.dist" with points
und solltet sehen, dass wir nicht ewig weit von Zipf’s Law weg sind.
(2)
Seht euch jetzt bigramModels.py an. Die drei Klassen für die Modelle sind hier interessant, wobei der eigentliche Kicker die
estimate-Methoden der ML- und GT-Bigramm-Modelle sind, die aus den gefeedeten Daten die Verteilungen der Bigramme schätzen.
Versucht, zu verstehen, was darin passiert.
Die Funktion runTest ist demgegenüber langweilig – sie fragt nach einer Eingabe und lässt dann die beiden Schätzer beurteilen, wie
wahrscheinlich die Eingabe unter den Schätzern ist.
Lasst das Programm laufen und seht nach, wie gut die beiden Modelle geeignet sind Tippfehler zu finden (wenn wir
das nach Bigrammodell wahrscheinlichere Wort als das richtige akzeptieren). Ganz aufschlussreiche Eingaben sind
z.B.
(hier
stimmen die Modelle überein, ” der“ ist besser. Na ja.)
(hier
versagt ML mit dem verwendeten Korpus, beide Wahrscheinlichkeiten sind Null, während Good-Turing das richtige Wort auswählen
würde)
(hier
liegen beide daneben, auch wenn GT immerhin der ersten, richtigen, Fassung nicht Wahrscheinlichkeit Null zuordnet. Aber natürlich
folgen diese Wörter nicht wirklich einem deutschen Sprachmodell)
(hier
liegen wieder beide richtig, wenn auch ML dem Wrot Wahrscheinlichkeit Null zuweist).
Ansonsten lasst eurer Fantasie freien Lauf; wenn ihr gute Beispiele habt, lasst es mich wissen – hier sind ein paar Vorschläge, die mich
so erreicht haben:
-
Sehenswürdigkeit – Sehenswrüdigkeit