17. Entropie

Leitfragen

Was ist Information? Warum ist unsere mathematische Definition nicht weit von einer intuitiven entfernt?
Warum brauchen wir Verteilungen, um Information definieren zu können?
Warum geht die Bestimmung von Entropie immer nur im Rahmen von Modellen?

Der Begriff der Entropie kommt ursprünglich aus der Thermodynamik und bedeutete dort etwas wie den Grad der Unordnung – eine Mischung aus Helium und Wasserstoff hat höhere Entropie als ein System, in dem die beiden Gase getrennt vorkommen.

Umgekehrt brauche ich bei hoher Ordnung weniger Information, um das Gesamtsystem zu beschreiben. Auf Datenströme (wie Sprachäußerungen) bezogen wird die Entropie dann gleich ein Maß für den Informationsgehalt.

Wie viel Information steckt in einer Nachricht? Modell für Nachricht: Folge von Zufallsvariablen X= X₁,…X_n. Annahme zunächst: Alle X_i unabhängig und mit P(X) identisch über X verteilt.

Wir werden nicht den Informationsgehalt einer Nachricht als solcher analysieren, sondern den der ihr zugrundeliegenden Verteilung. Hauptgrund dafür ist, dass wir Information statistisch definieren möchten und wir so nicht vom Ergebnis eines Zufallsexperiments ausgehen können – die Unterstellung ist: ” Wir können beliebig viele Nachrichten generieren“, und genau das geht natürlich nicht, wenn wir nur eine Nachricht haben.

Anschaulich gesprochen ist der Informationsgehalt einer Nachricht auch tatsächlich nicht zu bestimmen, ohne zu wissen, was noch alles (mit welcher Wahrscheinlichkeit) übermittelt werden kann. Im Extremfall enthält die Nachricht ” Ich habe eine Sechs gewürfelt“ gar keine Information, wenn nämlich der Würfel immer nur eine Sechs zeigt (und wir nicht am Zeitpunkt des Würfelwurfs interessiert sind).

Aber natürlich hindert uns niemand daran, aus einer konkreten Nachricht die zugrundeliegende Verteilung ihrer Bestandteile – so sie denn welche hat – zu schätzen und daraus eine Entropie der Nachricht zu bestimmen.

In diesem Sinne ist die Modellierung einer Nachricht bereits ein Spezialfall. Tatsächlich könnten wir, wenn wir etwa an der Entropie von Sprachäußerungen interessiert sind, einfach alle Äußerungen nehmen und eine Verteilung über sie ermitteln. Wenn wir allerdings diese Verteilung irgendwie sinnvoll bestimmen können, können wir auch den Lehrstuhl zumachen, denn dann hätten wir wohl alle Probleme der maschinellen Sprachverarbeitung gelöst…

Für ein vernünftiges Maß der Information H wollen wir:

H(X) ist in allen Werten von P(X) stetig (Wir wollen nicht, dass es plötzlich große Sprünge gibt, wenn wir nur ein ganz klein wenig an einer Wahrscheinlichkeit drehen)
H(X) wird für Gleichverteilung maximal (eine Abweichung von der Gleichverteilung teilt uns bereits einiges über X mit, das wir nicht mehr aus der Nachricht entnehmen müssen, d.h. der Informationsgehalt der Nachricht sinkt)
Information soll in einem gewissen Sinn additiv sein (für unabhängige Zufallsvariable soll H(X,Y) = H(X) + H(Y) gelten – um eindeutig auf die Entropie zu kommen, müsste diese Forderung noch etwas verschärft werden)

Ein Maß, das diese Forderungen erfüllt, ist die Entropie, konventionell definiert als

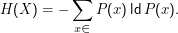
$H (X ) = - ∑x∈<strong><em>X</em></strong>P (x)ldP (x).$

Dabei bezeichnet ld den Logarithmus Dualis, den Logarithmus zur Basis 2. Nebenbei: Es gilt ldx= lnx∕ln2. Dass gerade die Basis 2 gewählt wurde (und darin, nicht in der funktionalen Form, liegt die Konvention), liegt daran, dass wir unsere Entropie in bits ausdrücken wollen, also in Informationseinheiten, die gerade zwei Zustände annehmen können. Wollten wir unsere Informationen in Dezimalzahlen ausdrücken und demnach bestimmen, wie viele Dezimalstellen zur Repräsentation der Daten nötig wären, könnten wir den dekadischen Logarithmus nehmen. Nur würde uns dann jedeR missverstehen.

Hinweis: P(x) ist nur eine Abkürzung für P(X= x). Manning und Schütze mögen diese Abkürzung in ihrem Abschnitt über Entropie noch nicht (wiewohl sie sie später durchaus verwenden), weshalb dort eine Funktion p:X→ℝ definiert wird durch p(x) = P(X= x).

Diese Definition sieht zunächst ein wenig beliebig aus. Das ist sie aber nicht. Betrachten wir dazu Zahlenraten, der Einfachheit halber von Zahlen ≤2ⁿ. Bei jedem Rateschritt gewinnen wir ein Bit Information (gesuchte Zahl ist kleiner/größer als geratene Zahl). Wie viele Rateschritte brauchen wir im schlimmsten Fall unbedingt (d.h. wenn wir maximal geschickt fragen)? Erste Frage: Größer als 2^n-1 ? Zweite Frage: Größer als A₁2^n-1 + 2^n-2? k-te Frage: Größer als ∑ _i=1^k-1A_i2^n-i + 2^n-k; dabei ist A_i = 1, wenn die i-te Frage bejaht wurde, 0 sonst. Wenn 2^n-k eins ist, wissen wir die Zahl (da wir nur ganze Zahlen raten und sich ganze Zahlen gerade um eins unterscheiden). Damit brauchen wir n binäre Fragen, um Zahlen bis 2ⁿ zu erraten.

Zusammenhang mit der Entropie: Sei die zu ratende Zahl x ein Wert einer Zufallsvariablen X, die auf {1,…,2ⁿ} gleichverteilt ist. Dann ist die Entropie von X gerade

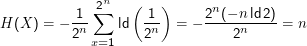
$n 1 2∑ ( 1 ) 2n (- n ld 2) H (X ) = ---n ld -n- = - -----n------= n 2 x=1 2 2$

– gerade die Anzahl der Fragen, die wir schlimmstenfalls brauchen. Ohne Gleichverteilung sinkt die Entropie, da wir ” geschickter“ fragen können, wenn wir wissen, dass bestimmte Zahlen sehr unwahrscheinlich sind (genauer beschäftigt sich damit die Codierungstheorie). Im Extremfall – es wird immer dieselbe Zahl x₀ genommen – ist P(X= x₀) = 1 und 0 sonst; die Entropie ist dann

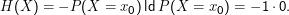
$H (X ) = - P (X = x0 )ld P (X = x0) = - 1 ⋅ 0.$

Wir brauchen gar keine Information mehr, um das Ergebnis zu kennen.

Man könnte verbieten, dass Null-Wahrscheinlichkeiten in den Verteilungen auftreten, es ist aber äquivalent und bequemer, 0log 0 = 0 zu definieren.

”Die Entropie ist der negative Erwartungswert der Logarithmen der Wahrscheinlichkeiten einer Verteilung“

Entropie von Sprache I

Sprachmodell I: X hat Werte aus ASCII, Buchstabe für Buchstabe. Wir schätzen P(X) aus gesammelten Artikeln der ” Zeit“ mit 4.5 ×10⁷ Zeichen und finden H(X) = 4.499.

Sprachmodell II: X entspricht Wörtern. Hier folgt H(X) = 12.03 aus 310791 verschiedenen Wörtern, was bei einer mittleren Wortlänge von 5.34 Buchstaben einer Entropie pro Buchstaben von 2.25 entspricht. Wie wir auf der nächsten Folie sehen werden, haben wir hier die reale Entropie vermutlich erheblich unterschätzt. Die Verwendung des Good-Turing-Schätzers für die Verteilung empfiehlt sich.

gzip-Test: Packer entfernen Redundanz (die definierbar ist als Differenz zwischen realer und maximaler Entropie; für byteorientierte Maschinen ist die maximale Entropie offenbar 8 bit pro Zeichen) aus Datenströmen. gzip -9 komprimiert den Korpus um einen Faktor 2.6, die ursprüngliche Entropie für gzip war also 8∕2.6 = 3.1.

Warum verschiedene Werte für H(X) für den gleichen Datenstrom? Wir bestimmen nicht wirklich die Entropie des Datenstroms, sondern die einer Verteilung, die wir aus dem Datenstrom schätzen. Dieser Verteilung liegt ein Modell zugrunde, das mehr oder weniger falsch ist. Sowohl für Wörter als auch für Buchstaben ist die Annahme gegenseitiger Unabhängigkeit aufeinanderfolgender X_i falsch, für Buchstaben offenbar falscher als für Wörter. Das Kompressionsprogramm gzip nutzt unter anderem diese Nicht-Unabhängigkeit, um Redundanz zu entfernen.

Zurück: Der Good-Turing-Schätzer III