18. Entropie II

Entropie von Sprache II

Einfachste Modellierung von Abhängigkeiten der Zeichen in einem Text: Folge X₁,…,X_n i.i.d. Zufallsvariablen mit Werten in den n-grammen. Es wird in der Regel auf die Entropie pro Zeichen normiert, die resultierende Entropie also durch n geteilt.

Warnung: Die Entropie von n-gram-Modellen ist schon für mäßige n praktisch nicht naiv zu berechnen, da die Verteilungen nur aus enormen Datenmengen zuverlässig zu schätzen sind.

Die maximale Entropie einer Verteilung über N elementaren Ausgängen ist die der Gleichverteilung, nämlich

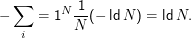
Um auf eine Entropie von 12 zu kommen, bräuchte man also schon im ” günstigsten“ Fall 2¹² = 4096 elementare Ausgänge, bei der Schätzung der Entropie pro Wort also verschiedene Wörter (Word Types). Wollte man eine Entropie von 12 bei einer realistischeren Nichtgleichverteilung erreichen, bräuchte man natürlich noch weit mehr verschiedene Zeichen (deren Wahrscheinlichkeiten dann aber auch noch mit einiger Zuverlässigkeit geschätzt werden müssen, was die Zahl der nötigen Word Tokens im Beispiel weiter in die Höhe treibt).

Wenn man einfach nur Wörter aus einem Text sammelt und daraus naiv die Verteilung schätzt, braucht man sehr lange Texte – unser Brumaire-Text etwa hat nur rund 6000 verschiedene Wörter, und selbst wenn deren Häufigkeiten ” richtig“ schätzbar wären, ist, weil wir eben nicht Gleichverteilung haben, nicht mit einer zuverlässigen Schätzung der wortbasierten Entropie des Englischen zu rechnen.

Übrigens hat Shannon als einer der Väter der Informationstheorie lange bevor es Rechner gab, die solche Schätzungen halbwegs zuverlässig hätten durchführen können, die wortweise Entropie des Englischen recht gut durch das ” Shannon game“ abgeschätzt: Man liest einen Teil eines Textes und lässt dann Menschen raten, was das nächste Wort wohl sei. Aus dem Verhältnis von richtigen zu falschen Antworten lässt sich die Entropie (über die Perplexität, s.u.) bestimmen.

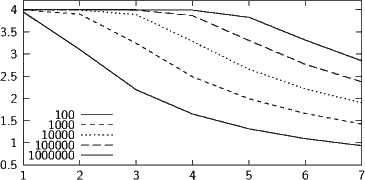
Die Grafik oben zeigt den Verlauf der geschätzten Entropie für zufällig generierte Strings mit 16 verschiedenen Symbolen, die alle gleiche Wahrscheinlichkeiten haben – die erwartete Entropie ist also immer ld16 = 4. Die verschiedenen Linien entsprechen Strings verschiedener Länge, also sozusagen der Korpusgröße.

Man sieht, dass alle Strings die 1-gram-Entropie ganz gut schätzen lassen. Schon für Bigramme liegt der 100er-Schätzer grob daneben. Es ist schon prinzipiell nicht möglich, dass er richtig schätzt, denn wir haben darin nur rund 100 Bigramme, also 100 elementare Ausgänge des Zufallsexperiments. Selbst wenn kein Bigramm doppelt vorkäme (was möglich ist, denn es gibt insgesamt 16² = 256 Bigramme über einem Alphabet von zwei Zeichen), wäre die Entropie der resultierenden Verteilung nur ld100 = 6.64. Die ” wahre“ Entropie der Verteilung ist demgegenüber 4 ⋅2 = 8. Trigramme werden noch vom 10000er-Schätzer halbwegs ordentlich behandelt. Das ist in diesem Fall auch zu erwarten, denn die maximale Entropie für 10000 gleichverteilte Ergebnisse, ld10000 = 13.29, liegt noch gut über der erwarteten Entropie 4 ⋅3 = 12. Bei 5-Grammen reichen dann auch 10⁶ Zeichen nicht mehr aus (selbst im unwahrscheinlichen günstigsten Fall nicht doppelt vorkommender 5-Gramme wäre das so, denn ld10⁶ = 19.93 ist immer noch kleiner als 4 ⋅5 = 20).

All diese Rechnungen gelten für die besonders freundliche Gleichverteilung mit nur 16 Zeichen. Reale Texte haben selbst nach großzügiger Vereinfachung deutlich mehr als 16 Symbole, und die Zahl der möglichen n-gramme geht exponentiell mit der Zahl der Symbole. Die Sprache hilft zwar ein wenig dadurch, dass die meisten n-gramme gar nicht auftreten (jedenfalls, solange man sich innerhalb einer Sprache bewegt) und daher die Gesamtzahl zu schätzender Wahrscheinlichkeiten nicht ganz 27ⁿ (oder was immer) ist, die aus obiger Figur sprechende Warnung gilt jedoch unvermittelt weiter – in der Tat habe ich das Experiment mit n= 16 gemacht, damit es überhaupt ein Referenzmodell gibt, für das die Entropie mit so naiven Methoden bestimmt werden kann.

Empirische Ergebnisse für einen Deutschen Text:

		Unigramm		Bigramm		Trigramm
		4.7		4.2		3.7

Modellierung von Abhängigkeiten

Will man Abhängigkeiten komplexer als durch n-gramme modellieren, brauchen wir Entropie für beliebig abhängige Z.V.s.

Ausgangspunkt: Sei P(x,y) die gemeinsame Verteilung von X und Y. Die gemeinsame Entropie von X und Y ist dann

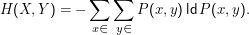
Daraus ableitbar: Die bedingte Entropie

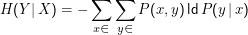
Wie kommt man darauf? Wir können schon die Entropie einer Verteilung einer Zufallsvariablen ausrechnen, also etwa

Die Additivität der Entropie liefert dann H(Y|X) = ∑ P(x)H(Y|x), was nach Einsetzen der Definition der bedingten Wahrscheinlichkeit – beachte P(x,y) = P(X= x∩Y= y) – und Ausklammern das obige Ergebnis liefert.

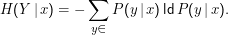
Es gilt die Kettenregel der Entropie:

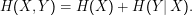
Das ist mit der Definition der bedingten Wahrscheinlichkeit P(x,y) = P(x)P(y|x) zu vergleichen – der Logarithmus macht auch hier eine Summe aus deinem Produkt.