Zurück zum letzten HMM-Problem: Wir haben eine Familie von HMMs (μϑ)ϑ∈Θ sowie eine Beobachtung O. Wir wollen ein ϑ0 finden, so dass P(O|μϑ0) maximal wird. Dabei ist für uns ϑ die Sammlung aller Werte von δ(i,j) und λ(i, j,o).
Warum sollte man das wollen? Nun, beim Schwarz-Weiß-HMM beispielsweise haben wir die Übergangs- und Emissionswahrscheinlichkeiten aus dem Bauch heraus geschätzt. Tatsächlich ließe sich aber die ” Verrauschtheit“ des Druckers aus Beobachtungen schätzen, so dass man ein quasi auf den vorliegenden Drucker optimiertes HMM erhält.
Man ahnt schon, dass dies stark auf EM hinausläuft, und das ist auch so. Das Äquivalent zu den Mitgliedswahrscheinlichkeiten der GMMs sind hier die ” Wichtigkeiten“ der einzelnen Übergänge im HMM unter einer bestimmten Beobachtung. Sie lassen sich so berechnen, wenn wir – wie gehabt – schon ein Anfangsmodell haben:
Sei pt (i,j) = P(Xt = i,Xt + 1 = j|O,μ). In unseren Forward-Backward-Variablen ist
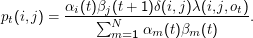
Woher kommt diese Formel? Zunächst ist
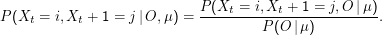
Die Wahrscheinlichkeit für einen Übergang von i zum Zeitpunkt t nach j zum Zeitpunkt t+ 1 unter Emission von ot (also der Zähler) ist einfach die die Wahrscheinlichkeit, dass wir zu t im Zustand i sind (αi(t)) mal der Wahrscheinlichkeit, dass es von j aus weitergeht (βj (t+ 1)) mal der Übergangswahrscheinlichkeit von i nach j (δ(i,j)) mal der Wahrscheinlichkeit, dass bei diesem Übergang das richtige Zeichen emittiert wird (λ(i,j,ot)). Der Nenner ist einfach wieder eine Normierung.
Im M-Step nehmen wir wieder eine geeignete Mittelung vor, diesmal über die verschiedenen Schritte des HMM.
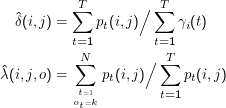
Es ist nicht ganz leicht, einzusehen, dass das Modell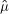 
= (
,
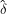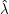) wirklich die Ungleichung
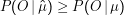
Wie schon bei den GMMs heißt Konvergenz des Forward-Backward-Verfahrens noch lange nicht, dass wir das beste oder auch nur ein gutes Modell gefunden haben. Dazu kommt, dass es je nach Typ des HMM nichttrivial ist, gleichzeitig auf mehrere Beobachtungen zu trainieren (was aber natürlich in der Regel nötig ist). Deshalb: Training von HMMs nur mit Vorsicht und am Besten nach Studium einschlägiger Literatur (der Industriestandard dazu ist Mitchell: Machine Learning).
Es gibt übrigens etliche Alternativen zu Forward-Backward, wenn man HMMs anpassen will, etwa geeignet eingeschränkte Monte-Carlo-Methoden, bei denen zufällig Punkte im Parameterraum probiert werden, oder genetische Algorithmen, in denen durch Mutation und Selektion Parametersätze quasi evolutionär verbessert werden – in der Regel dürfte Forward-Backward aber der geeignetste Algorithmus sein.
Der Nutzen von HMMs
HMMs werden in der Computerlinguistik zu vielen Zwecken eingesetzt. Ihren Durchbruch hatten sie wohl in der Erkennung gesprochener Sprache. Dabei sind die Symbole, die das HMM emittiert, ”Merkmalsvektoren“, die durch geeignete Filter aus kleinen Stückchen der Sprachaufnahme gewonnen werden, während die Zustände etwa Phonen oder gar Phonemen entsprechen können (in der Realität ist das nicht ganz so einfach, und in der Regel ist die Menge der Merkmalsvektoren auch nicht diskret, so dass die Emissionswahrscheinlichkeiten aus Dichten bestimmt werden müssen – unsere Algorithmen funktionieren aber normal weiter).
Große Popularität haben HMMs auch im Tagging, d.h. in der Erkennung von Wortklassen (Nomen, Verb, Artikel,… ). Dabei ist klar, dass in einem grammatisch korrekten Satz normalerweise nicht jede beliebige Wortart hinter jeder beliebigen anderen kommen wird – und dies ist die Abhängigkeit, so dass schon klar ist, dass die Zufallsvariablen Werte in den Wortklassen annehmen. Die Ausgabesymbole können tatsächlich die word tokens sein, womit allerdings die Zahl der zu schätzenden Parameter extrem groß wird.
Tatsächlich empfehle ich zum Taggen eine andere, mathematisch nicht ganz so wohlfundierte (und deshalb nicht hierhergehörende… ), dafür aber linguistisch wohlmotivierte, Technik namens Transformation Based Learning. Die bekannteste Implementation eines TBL-Taggers ist der Brill-Tagger.