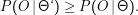33. Exkurs: Expectation Maximization
Wenn wir
lösen
wollen, müssen wir wissen, welche Datenpunkte zu welchen Gaussians gehören. Um das zu bestimmen, müssten wir allerdings die
Gaussians schon kennen.
Ausweg aus diesem Henne-Ei-Problem: Expectation Maximization. Wir nehmen einfach ein paar Gaussians an und bestimmen daraus
die Wahrscheinlichkeiten für die Zugehörigkeit (E-Step):
P(
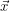 i
i |
φj) ist dabei einfach als der Wert von
φj an der Stelle
xi zu berechnen, und der Nenner ist eine schlichte Normierung, die man
in tatsächlichen Implementationen besser im Nachhinein macht.
Mit diesen Daten maximieren wir die Likelihood (M-Step). Das neue Zentrum eines φj ist das mit den Mitgliedswahrscheinlichkeiten
gewichtete Mittel der Positionen der Datenpunkte:
Die neuen Breiten ergeben sich aus dem gewichteten Mittel der Quadrate der neuen Ablagen:
Hier
soll
σjk die
k-te Komponente von
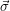 j
j bedeuten und analog für die übrigen Vektoren.
Wenn man so abschätzt und das entstandene Modell Θ‘ nennt, kann man zeigen:
Bei
jeder Anwendung von EM sollte sich also die Likelihood der Punkte unter dem Modell erhöhen (oder jedenfalls nicht schrumpfen).
Damit läuft man immer auf einen ” Gipfel“ der Landschaft auf der letzten Folie zu.
Es ist sehr gut möglich, dass dies nicht das globale Maximum ist – das hängt letztlich von der Stelle ab, an der man anfängt. Deshalb
ist bei EM ein ” gutes“ Anfangsmodell häufig extrem wichtig, um ein ” Hängenbleiben“ in einem lokalen Maximum zu
vermeiden.
Mehr zur Frage der Abhängigkeit des Ergebnisses der EM von den Anfangswerten kann man beim Spielen mit den Programmen im
Anhang erfahren – im Allgemeinen muss die Wahl der Anfangswerte mit domänenspezifischen Methoden erfolgen. Häufig
kann ein weniger empfindliches Verfahren wie K-Means helfen. Aber dies ist nicht mehr Thema dieser Veranstaltung.
Übungen zu diesem Abschnitt
Ihr solltet euch wenigstens an den rötlich unterlegten Aufgaben versuchen
(1)
Holt euch das Programm gaussMixtures.py von der Webseite zur Vorlesung.
Macht euch zunächst mit der Gaussian-Klasse vertraut; sie implementiert im wesentlichen die mehrdimensionalen
Normalverteilungen aus dem Skript.
Ein paar Tricks sind aber schon dabei: Erstens kocht setSigmas die Standardabweichungen vor, so dass die Berechnung des
Wertes (in der __call__-Methode, die bewirkt, dass man einen Gaussian einfach als Funktion verwenden kann) nicht
unnötig viel rechnen muss. Dann kann man eine Grenze angeben, unter die keine Komponente von Sigma schrumpfen
kann. Das ist ein Trick, um zu verhindern, dass das Programm stirbt, wenn sich ein Gaussian auf einen einzelnen
Punkt festfrisst (was er so oder so besser nicht tun sollte… ). Die draw-Methode verwendet eine Funktion aus der
random-Bibliothek von Python, um Punkte zu erzeugen, die, wenn man oft genug zieht, entsprechend dem Gaussian
verteilt sind. Das geht hier einfach, weil wir effektiv unabhängige eindimensionale Verteilungen haben. Darüber hinaus
kann ein Gaussian, wenn man ihm in der update-Methode sagt, für welche Punkte er sich wie verantwortlich fühlen
soll, ein neues Zentrum und neue Sigmas für sich berechnen (das ist der Maximize-Step aus dem EM-Algorithmus)
(2)
Seht euch die DistMixture-Klasse an. Neben etlichen technischen Geschichten (addDistribution, removeDistribution,
__iter__) ist hier die Logik für die EM enthalten. Seht euch _runEStep und _runMStep an und versucht zu sehen, dass
diese gemeinsam mit Gaussian.update das tun, was im Skript beschrieben wurde. Wichtig dazu ist die Funktion
computeWeightedMean, die eben ein gewichtetes Mittel ihres ersten Arguments berechnet. Dass wir hier mit den Punkten (also mit
Vektoren) so bequem rechnen können, liegt daran, dass wir in Point die einschlägigen Operatoren Pythons so umdefiniert haben, dass
sie das tun, was wir für Punkte gerne hätten. Die Details sind aber nicht so wichtig.
Schließlich solltet ihr noch einen Blick auf getTotaLogL werfen, das die log-likelihood für eine Punktmenge unter dem Modell liefert,
und auf getMostLikelyCluster, das einfach den Gaussian zurückgibt, der für den übergebenen Punkt p den größten Wert hat
(also argmaxφφ(p)).
(3)
Sorgt dafür, dass am Fuß des Programms die Funktion testWithGUI aufgerufen wird und lasst das Programm laufen.
testWithGui baut eine GaussianMixture, die absichtlich etwas ambig ist; die Komponenten dieser Mixture seht ihr als farbige
Ellipsen, die die 1-σ-Linien repräsentieren. Dazu werden 100 Punkte erzeugt, die nach dieser GM verteilt sind. Seht euch zunächst an,
was die EM in dieser Situation tut – der SStepKnopf (oder die Leertaste) macht jeweils einen Schritt. Die log likelihood in der
Statuszeile sollte dabei wachsen (sie wird negativ sein, der Betrag der Zahl sollte also abnehmen). Das wird in der Realität nicht immer
so sein, was an Numerikproblemen liegt.
Nach einigen (in der Regel wenigen) Schritten sollte sich nicht mehr viel tun. Warum hat sich überhaupt etwas verändert? Tipp: Seht
mal, wie viel sich tut, wenn ihr, bevor ihr die EM laufen lasst, mit dem Knopf ” 1000 Points“ entsprechend mehr Punkte erzeugt und
also die Verteilung besser beschreibt. Mit unseren öden Poolmühlen ist es allerdings kein Spaß, dem Rechner zuzusehen
(Re-Implementation in C könnte helfen:-)
(4)
Vielleicht hilft es beim Verständnis der EM, sich die vermutete Zugehörigkeit von Punkten zu einzelnen Gaussians zeigen zu lassen.
Klickt dafür auf den ” Colour“-Knopf. Die Farben der Punkte geben danach den Grad der Zugehörigkeit der Punkte zu den
verschiedenen Gaussians an. Die Farbdarstellung braucht allerdings viel Rechenzeit. Es kann sich lohnen, das Programm auf ella laufen
zu lassen.
(5)
Wenn ihr mit der rechten Maustaste auf eine Ellipse klickt, könnt ihr den zugehörigen Gaussian löschen. Mit der linken
Maustaste und ziehen könnt ihr neue Gaussians erzeugen. Auf diese Weise könnt ihr die Anfangsbedingungen der EM
verändern.
Versucht, mit verschiedenen Anfangsbedingungen verschiedene Ergebnisse für die gleiche Punktmenge herauszukitzeln – technisch
landet ihr in verschiedenen lokalen Maxima, wenn ihr das hinkriegt. Es sollte nicht schwierig sein, wenn doch, könnt ihr mit der
mittleren Maustaste Punkte hinzufügen.
Lustig ist auch, einen Gaussian mit großer und einen mit kleiner Breite zu erzeugen und zu sehen, wie der große Punkte ” hinter“ dem
kleinen adoptiert (” Colour“ – das funktioniert übrigens nur bis zu drei Gaussians, weil es nicht mehr Grundfarben zum Mischen gibt).
(6)
Wir wollen jetzt eine Art ” semantisches Clustering“ machen. Die Idee dabei ist, aus den Kontexten von Wörtern auf
Bedeutungszusammenhänge zu schließen; Wörter werden also durch die word types, die in ihrer Nachbarschaft gefunden werden,
dargestellt, und deren Frequenzen sind die Featurevektoren. Ein Programm, das Featurevektoren aus einem Korpus zieht, ist auf der
Webseite zu bekommen, ist aber eher zum daheim Spielen gedacht. Für Tutoriumszwecke habe ich bereits Featurevektoren für die
Wörter
blue
horse
apple
stream
car
nut
pear
lake
unhappy
sad
creek
carriage
green
boat
merry
orange
white
river
red
happy
aus einem Jahrgang Project Gutenberg extrahiert und ebenfalls auf die Webseite gestellt (die erste Zeile erlaubt die Zuordung der
einzelnen Dimensionen zu diesem Raum zu den Kontextwörtern, deren Counts sie angeben – die Vektoren sind außerdem bereits
normalisiert, so dass wir effektiv in einem Raum der Dimension |Kontextwörter|-1 Clustern).
Probiert zunächst selbst, die Wörter oben nach ” Verwandtschaft“ zu gruppieren.
Probiert es danach mit EM. Zuständig dafür ist die Funktion testWithFeatureVectors, in der ihr den Haufen langweiliger
Hilfsfunktionen ignorieren könnt. Für unsere Zwecke interessant ist nur buildMixture. Die Funktion nimmt von der Kommandozeile
die Namen der Anfangszentren der neuen Cluster (sowas ließe sich im Prinzip auch automatisch bestimmen, aber besser ist es immer,
wenn man dem Rechner hier ein wenig hilft). Das erste Kommandozeilenargument ist der Name der Datei mit den
Featurevektoren.
Probiert also, was
python gaussMixtures.py features car sad apple river blue
ausgibt – das sind zunächst die log likelihoods, bis das Programm beschließt, dass sich die Situation beruhigt hat. Danach
werden die Werte der einzelnen Gaussians für die einzelnen zu clusternden Worte ausgegeben und schließlich die Cluster
selbst.
Probiert, was passiert wenn ihr andere Wörter angebt, oder mehr oder weniger davon. Ihr solltet sehen, dass die Anfangsbedingungen
bei EM entscheidend wichtig sind und die P(Θ|O)-Landschaft wirklich viele Hügel hat.
Dateien zu diesem Abschnitt
Markus Demleitner
Copyright Notice
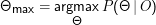
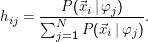
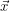 i |φj) ist dabei einfach als der Wert von φj an der Stelle xi zu berechnen, und der Nenner ist eine schlichte Normierung, die man
in tatsächlichen Implementationen besser im Nachhinein macht.
i |φj) ist dabei einfach als der Wert von φj an der Stelle xi zu berechnen, und der Nenner ist eine schlichte Normierung, die man
in tatsächlichen Implementationen besser im Nachhinein macht.
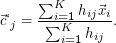
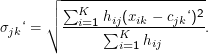
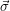 j bedeuten und analog für die übrigen Vektoren.
j bedeuten und analog für die übrigen Vektoren.