32. Exkurs: Gaussian Mixtures

Bevor wir das Problem des ” besten“ Modells für eine Beobachtung angehen können, sehen wir zunächst ein – scheinbar ganz anderes – Problem an: Soft Clustering.

Idee des Clustering ist, zusammenhängende Datenpunkte zu erkennen. Anwendungen dafür gibt es viele: z.B. will man in der Spracherkennung ” ähnliche“ Klänge gruppieren, bei der Disambiguierung word tokens den verschiedenen Lesungen des word types zuordnen, im information retrieval Dokumente klassifizieren usf. Die Idee dabei ist in der Regel, die Datensätze in Vektoren zu verwandeln, die feature vectors (für die Mixtures, die wir hier haben, ist das allerdings nicht notwendig – solange wir berechnen können, wie wahrscheinlich es ist, dass eine Beobachtung von einem ” Cluster“ erzeugt wird, können wir rechnen).

Bei Dokumenten oder bei der Desambiguierung entspricht dabei jedem Eintrag im Vektor einfach, wie oft ein word type im Dokument oder in den Umgebungen der zu clusternden Wörter vorkommt – mithin braucht der Raum, in dem man clustert, so viele Dimensionen, wie man word types hat. Danach probiert man einfach, in irgendeinem Sinne benachbarte Punkte im Raum zusammenzufassen und von denen abzugrenzen, die nicht benachbart sind.

Wenn ihr findet, dass dieses Problem eng mit der Klassifikation verwandt ist, liegt ihr richtig. Etwas vereinfacht könnte man sagen, Clustering sei letztlich Klassifikation ohne Trainingsdaten.

Eine populäre Methode zum Clustering verwendet Gaussian mixture models (GMMs), Summen von gewichteten Normalverteilungen. Weil wir d-dimensionale Räume betrachten, brauchen wir auch mehrdimensionale Normalverteilungen. Für uns reichen Normalverteilungen mit diagonaler Kovarianzmatrix:

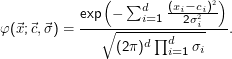
Das ist schlicht ein Produkt von d Normalverteilungen in den d Dimensionen (im Exponenten wird das Produkt zu einer Summe).

In Wirklichkeit ist die hier angegebene Familie von Normalverteilungen ein Spezialfall. Letztlich nämlich definieren die Werte von 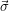die Breiten der Gaußverteilungen in den verschiedenen Richtungen des Raumes. Wenn man sich das zunächst in der Ebene vorstellt, sieht man, dass die Linien gleicher Werte dieser Verteilungen etwas wie Ellipsen bilden, dass diese Ellipsen aber ihre Hauptachsen immer parallel zu den den Achsen des Koordinatensystems haben. Es ist aber einfach, sich ein paar Punkte auf die Ebene zu malen, die besser durch Normalverteilungen mit ” schräg“ stehenden Ellipsen zu beschreiben wären. Was tun?

Die Lösung ist, von 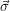zu einer d×d-Matrix Σ überzugehen (wären wir streng, hätten wir übrigens genau umgekehrt vorgehen müssen). Die Details werden hier etwas haarig, und wer sich dafür interessiert, sollte Vorlesungen in Linearer Algebra besuchen und dort besonders bei ” Eigenwerttheorie“ aufpassen. Die Anwendung jedoch ist zwar recht rechenaufwändig, aber nicht wirklich schwer. Jedenfalls sehen diese von der Fixierung auf die Koordinatenachsen befreiten Normalverteilungen so aus:

Darin bezeichnen |Σ| und Σ^-1 die Determinante und die Matrixinverse von Σ (wiederum verweise ich auf die Lineare Algebra), das hochgestellte T bedeutet einfach Transposition (aus einem Spaltenvektor wird ein Zeilenvektor, was es hier braucht, um die Matrixmultiplikation durchführen zu können). Wer LA hinter sich hat, sollte recht schnell sehen, dass sich diese Formel auf die oben angegebene zurückführen lässt, wenn Σ nur Einträge in der Diagonalen hat, und daher kommt auch der Name der Verteilungen oben.

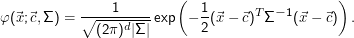
Wer wirklich optimale Anpassung einer mehrdimensionalen Normalverteilung auf gegebene Daten haben möchte, kommt natürlich nicht um die Verwendung der ” richtigen“ Normalverteilung herum. In den meisten Fällen sind aber die diagonalen Kovarianzmatrizen ” gut genug“ (d.h. bieten einen guten Kompromiss aus Anpassungsvermögen und Einfachheit).

Eine Gaussian Mixture Θ ist nun ein Modell von N solchen Verteilungen, die noch gewichtet sein können. Es ist die Gesamtwahrscheinlichkeit eines Datenpunktes 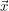unter Θ:

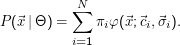
Darin steht π_i für die a-priori-Wahrscheinlichkeit, dass gerade die i-te Verteilung ” zum Zug“ kommt. Das Bild ist hier wieder, dass die Beobachtung vom Modell erzeugt wurde – wenn nun eine Komponente der mixture nur ein kleines π_i hat, wird sie nur seltener ausgewählt und weniger Punkte werden von ihr erzeugt.

Wir haben jetzt eine Beobachtung O= {x_i,i= 1…K}. Die beste Erklärung dieser Beobachtung durch ein GMM finden wir durch

Die Maximierung läuft dabei normalerweise über alle möglichen GMMs mit der gewählten Zahl von Komponenten und d Dimensionen. Es ist aber auch durchaus denkbar, verschiedene Komponentenzahlen zuzulassen. Wenn wir keine speziellen Erwartungen an Θ haben – dies ist der Normalfall, wenn wir nur GMMs gleicher Länge betrachten –, also der Prior P(Θ) die Gleichverteilung ist, können wird auch gleich P(O|Θ) maximieren.

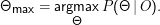
Das Problem:

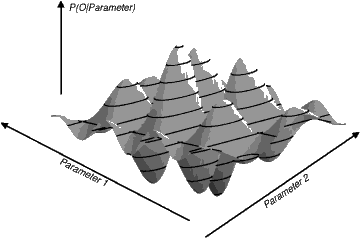
Schon bei zwei Parametern kann die ” Landschaft“, in der wir nach dem Maximum suchen, beliebig kompliziert sein. Es gibt kein analytisches Verfahren zur Suche nach dem Maximum.