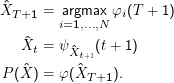31. Der Viterbi-Algorithmus
Der Viterbi-Algorithmus findet zu jeder Beobachtung O die wahrscheinlichste Zustandsfolge X, die ein HMM bei der Ausgabe von O
genommen hat.
Wir definieren uns ein Trellis
φj (t) enthält also an jeder Stelle die Wahrscheinlichkeit des wahrscheinlichsten Weges, der unter Emission von o1 ot-1 zum
Zustand j zur Zeit t führt. Wir brauchen aber noch zusätzlich die Information, welcher Weg das war. Diese Information wird uns das
unten definierte zweite Trellis ψ liefern.
ot-1 zum
Zustand j zur Zeit t führt. Wir brauchen aber noch zusätzlich die Information, welcher Weg das war. Diese Information wird uns das
unten definierte zweite Trellis ψ liefern.
Die Initialisierung ist wie gewohnt: φi(t) = δij mit dem Startzustand j.
Wir arbeiten uns nach vorne durch,
und
merken uns, woher wir jeweils gekommen sind:
Der Operator argmax bestimmt das Argument des Maximalwerts, wobei das Argument das ist, worüber die Maximierungsoperation
läuft. Im Fall oben ist das das i, so dass wir in ψ gerade speichern, woher unser φ kam. Wir werden das brauchen, um uns wieder
zurückzuhangeln.
Wenn unsere beiden Trellises gefüllt sind, suchen wir von hinten startend die wahrscheinlichste Sequenz 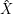 :
:
Trellise
im Viterbi-Algorithmus für die Eingabe 01011100 und unser Schwarzweiß-HMM:
|
oj
|
| φ
| ψ
|
|
W
|
B
|
E
|
W
|
B
|
E
|
|
0
|
0.0
|
-
|
-
|
-
|
-
|
-
|
|
1
|
0.40
|
1.3
|
-
|
W
|
W
|
-
|
|
0
|
1.4
|
0.74
|
2.6
|
W
|
W
|
B
|
|
1
|
1.8
|
2.0
|
1.1
|
W
|
B
|
B
|
|
1
|
2.8
|
2.1
|
1.8
|
W
|
W
|
E
|
|
1
|
3.8
|
2.5
|
2.5
|
W
|
B
|
E
|
|
0
|
4.8
|
2.8
|
3.2
|
W
|
B
|
E
|
|
0
|
5.2
|
4.1
|
3.2
|
W
|
B
|
B
|
|
-
|
5.6
|
5.4
|
3.3
|
W
|
B
|
E
|
Die Wahrscheinlichkeiten sind als negative dekadische Logarithmen gegeben, 4.61 bedeutet etwa 10-4.61 ≈2.45 ×10-5. Für so
kleine Zahlen ist das bequemer, und in der Tat lohnt es sich, den Viterbi-Algorithmus komplett in Logarithmen zu
implementieren.
Ein - als Quellzustand bedeutet, dass es keinen Weg zum entsprechenden Zustand gibt. Da unsere HMMs beim Übergang
emittieren, durchlaufen sie für n Eingabezeichen n+ 1 Zustände, weshalb beim letzten Eingabezeichen nur ein Strich
steht.
Readout (von hinten): E, E, B, B, B, W, W, W mit Wahrscheinlichkeit 10-3.3. Der schwarze Strich geht wahrscheinlich von Spalte 4
bis Spalte 6.
Dabei interessiert uns jeweils der Zustand, in den das System auf dem wahrscheinlichsten Pfad bei ” Emission“ des jeweiligen Zeichens
gegangen ist. Ganz am Schluss war das ein E. Dessen Quelle war laut ψ wieder ein E (in der Zeile darüber), dessen Quelle wiederum ein
B und so weiter. Für die erste Zeile schreiben wir gar keinen Zustand auf, da ja das System hier noch gar kein Zeichen gelesen hatte,
um in den Zustand zu kommen.
Übungen zu diesem Abschnitt
Ihr solltet euch wenigstens an den rötlich unterlegten Aufgaben versuchen
(1)
Besorgt euch das Programm hmm.py von der Vorlesungsseite. Das Programm benötigt das markovmodel-Modul von der Folie
”Markov-Ketten“.
Seht euch darin die HMM-Klasse an. Sie macht zunächst für die Ausgabesymbole, was die MarkovModel-Klasse schon für die Zustände
gemacht hat: Die Ausgabesymbole werden aufgezählt, so dass wir intern nur noch Zahlen zwischen 0 und n-1 verwenden
( computeEmissionMapping).
Das ist für ein nacktes Markov-Modell kein großer Vorteil, hilft aber, wenn wir nachher unsere ” Standardfragen“ beantworten wollen.
Ebenfalls analog zu MarkovModel berechnen wir sowohl eine Übergangsverteilung (_computeEmissionMatrix) als auch
Verteilungsfunktionen für die Ausgaben der Übergänge, die wir wieder beim Generieren brauchen (_computeOutputDfs) und die
nach Notwendigkeit von driveOn aufgerufen wird. driveOn wiederum greift auf das driveOn des MarkovModels zu und
berechnet zusätzlich die Ausgaben.
(2)
Probiert die HiddenMarkovModel-Klasse aus. Folgende Beschreibung baut einen HMM ähnlich dem in der Vorlesung besprochenen für
einen schwarzen Streifen:
{
"whitebefore": {"blackstrip": 0.1, "whitebefore": 0.9},
"blackstrip": {"whiteafter": 0.1, "blackstrip": 0.9},
"whiteafter": {"whiteafter": 1},
}
---
{"whitebefore": 1}
---
+whitebefore-whitebefore+ {'0': 0.8, '1': 0.2}
+-+
+whitebefore-blackstrip+ {'1': 0.9, '0': 0.1}
+-+
+blackstrip-blackstrip+ {'1': 0.9, '0': 0.1}
+-+
+blackstrip-whiteafter+ {'1': 0.1, '0': 0.9}
+-+
+whiteafter-whiteafter+ {'0': 0.8, '1': 0.2}
+-+
Schreibt das in eine Datei, deren Inhalt ihr dem HMM-Konstruktor übergebt, ruft dessen setUpInitDf-Methode auf und
lasst euch das Resultat der getAnOutput-Methode für, sagen wir, 30 Schritte ausgeben. Erklärt, was ihr seht.
(3)
Bei den meisten nützlichen Anwendungen von HMMs hat man als Trainingsdaten die versteckten Variablen zusammen mit der
Ausgabe (z.B. handgetaggte Korpora). Unter diesen Umständen braucht man kein EM-Training, sondern kann einfach die relevanten
Parameter des HMM (Übergangs- und Emissionswahrscheinlichkeiten) schätzen. Wir wollen das hier schlicht mit ML machen (warum
wäre für das Pixelstreifen-Modell SGT nicht gut?).
Seht euch die Funktion estimateModelParameters an – sie will eine Liste von Listen der Art, wie sie HMM.getAnOutput
zurückgibt. Erzeugt euch also einen Schwung Ausgaben, übergebt sie an estimateModelParameters und seht, wie gut die
Schätzung so wird.
estimateModelParameters tut so, als würde es eine Eingabe für den Konstruktor von HMM ausgeben. Dabei fehlt allerdings die
Anfangsverteilung. Vielleicht wollt ihr das ja noch nachrüsten?
(4)
Um zu sehen, wie viel man von Viterbi erwarten kann, wollen wir jetzt die tatsächlich von einem gegebenen HMM durchlaufenen
Zustandsfolgen mit dem vergleichen, was Viterbi ausgibt. Das wird von probD gemacht. Versucht, zu verstehen, was diese Funktion tut
und probiert sie dann aus. Damit die Ausgabe etwas übersichtlicher wird, ist es klug, die versteckten Zustände oben umzubenennen,
etwa so:
{
"(": {"_": 0.1, "(": 0.9},
"_": {")": 0.1, "_": 0.9},
")": {")": 1},
}
---
{"(": 1}
---
+(-(+ {'0': 0.8, '1': 0.2}
+-+
+(-_+ {'1': 0.9, '0': 0.1}
+-+
+_-_+ {'1': 0.9, '0': 0.1}
+-+
+_-)+ {'1': 0.1, '0': 0.9}
+-+
+)-)+ {'0': 0.8, '1': 0.2}
+-+
Überlegt euch, warum es gar nicht zu erwarten ist, dass der Viterbi die tatsächliche Zustandsfolge immer findet. Versucht, die Irrtümer
zu erklären.
Dateien zu diesem Abschnitt
- hmm.py --
Eine Implementation von HMMs inklusive Forward und Viterbi
Markus Demleitner
Copyright Notice
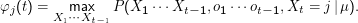
 ot-1 zum
Zustand j zur Zeit t führt. Wir brauchen aber noch zusätzlich die Information, welcher Weg das war. Diese Information wird uns das
unten definierte zweite Trellis ψ liefern.
ot-1 zum
Zustand j zur Zeit t führt. Wir brauchen aber noch zusätzlich die Information, welcher Weg das war. Diese Information wird uns das
unten definierte zweite Trellis ψ liefern.
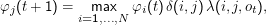
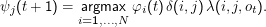
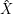 :
: