Backward procedure
Wir können auch umgekehrt bedingen:
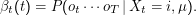
Die Frage ist jetzt also: Wie groß ist die Wahrscheinlichkeit, dass wir ot
oT beobachten werden, wenn wir zum Zeitpunkt t im
Zustand i sind? Im Vergleich zur ” forward procedure“ haben wir jetzt Wahrscheinlichkeiten für etwas, das wir noch
beobachten werden, unter der Bedingung, dass wir jetzt in einem bestimmten Zustand sind, während wir bei den αi die
Wahrscheinlichkeit dafür berechnet haben, dass wir in einem bestimmten Zustand sind, wenn wir etwas beobachtet
haben.
Diese Umkehrung hat für sich keinen wirklichen Sinn, wird uns aber beim Trainieren von HMMs sehr helfen.
Am Ende der Beobachtung ist es sicher, dass wir nichts mehr beobachten, also
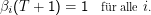
Wir arbeiten uns von dort aus nach vorne durch:
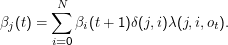
Die totale Wahrscheinlichkeit ist dann βk(1), wenn k der Index des Startzustands ist.
Wieder mag ein Bild helfen:
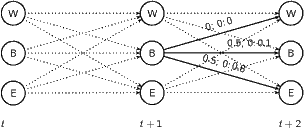
Nehmen wir an, dass t+ 2 der letzte Schritt ist. Dann sind alle βi(t+ 2) = 1. Die Wahrscheinlichkeit, dass wir 0 beobachten werden, wenn wir zum Zeitpunkt t+ 1 im Zustand 2 sind, ist
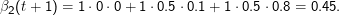
Die beste Zustandsfolge
Die zweite Frage: Was ist die beste Zustandsfolge, um eine gegebene Beobachtung zu erklären?
Naiv: Einfach zu jedem Zeitpunkt t das xt suchen, für das P(Xt = xt|O,μ) maximal wird.
Im Einzelfall kann das sinnvoll sein. Im Allgemeinen wollen wir aber nicht ∏ t=0T+1P(Xt = xt|O,μ) maximieren, sondern P(X1 = x1,…XT+1 = xT+1 |O,μ).
Diese beiden Größen sind verschieden, weil die Xt nach Definition der Markowkette nicht unabhängig voneinander sind.
Für drei Zustände könnte das so aussehen:
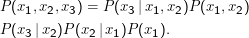
Dabei habe ich erstens alle ” konstanten“ Abhängigkeiten weggelassen (O und μändern sich während der Berechnung nicht) und zweitens wieder Xi = xi als xi abgekürzt. Solche Geschichten werden in der Literatur gern gemacht, weil sonst alle Ölquellen Saudi-Arabiens nur noch für die Produktion von Druckerschwärze sprudeln müssten.
Das ist nur dann gleich P(x1)P(x2)P(x3), wenn P(xi+1 |xi) = P(xi+1) ist. Das wiederum ist nur dann der Fall, wenn Xi und Xi+1 unabhängig sind, wir also gar kein Markov-Modell, sondern i.i.d. haben. Wer es nicht sieht:
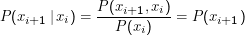
Wenn wir also die ” beste“ Zustandsfolge in einem Markov-Modell finden möchten, müssen wir einen Ausdruck mit all den bedingten Wahrscheinlichkeiten ausrechnen. Die Standardmethode wurde von Andrew Viterbi entwickelt und ist unser nächstes Thema.