29. Standardmethoden von HMMs I

Praktisch alle Anwendungen von HMMs beruhen auf der Beantwortung von folgenden Fragen:

1. Wie wahrscheinlich ist eine Beobachtung O in einem gegebenen Modell μ?
2. Was ist die wahrscheinlichste Erklärung für die Beobachtung O unter einem Modell μ?
3. Sei eine Beobachtung O und ein Menge M= {μ(ϑ)|ϑ∈Θ} möglicher Modelle gegeben. Welches Modell μ(ϑ₀) erklärt O am besten?

Wir sprechen hier immer von Beobachtung, wo wir vorher von Ausgabe gesprochen haben; Hintergrund ist, dass HMMs fast nie zur Generierung von Sequenzen verwendet werden, sondern fast immer zur a-posteriori-Erklärung von beobachteten Sequenzen. Das ist auch der Hintergrund des Wortes ” hidden“: Man sieht nur das Ergebnis des HMM, die Folge der Zustände ist zunächst versteckt.

Die dritte Frage stellt sich im Allgemeinen als Lernproblem. Wir haben viele Beobachtungen und wollen zunächst ein HMM trainieren, die Parameter (ϑ wird meist vektorwertig sein) also so einstellen, dass sie den Beobachtungen maximal gut angepasst sind. Mit dem trainierten HMM können dann Fragen vom Typ 2 beantwortet werden.

Das erste Problem

Was ist die Wahrscheinlichkeit für eine Beobachtung O?

Eigentlich einfach: Wir rechnen für alle möglichen Zustandsfolgen X= (X₁,…,X_T+1) die individuellen Wahrscheinlichkeiten P(O|X,μ) aus und addieren sie.

Diese Wahrscheinlichkeiten sind tatsächlich einfach auszurechnen.

wobei o_t das zwischen t und t+ 1 emittierte Zeichen ist. Die Bedingung auf μ ist hier natürlich eigentlich überflüssig, da wir im Augenblick ohnehin immer nur ein Modell haben.

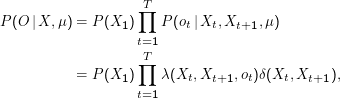
Es ist nicht schwer zu zeigen, dass die einzelnen P(O|X,μ) unabhängig sind, also eine schlichte Addition dieser Größen die gesuchte Gesamtwahrscheinlichkeit liefert.

Problem: Laufzeit ist ewig, man braucht (2T+ 1)N^T+1 Multiplikationen für N Zustände.

Dynamic Programming

Abhilfe ist das dynamic programming. Idee dabei ist, einmal berechnete Werte in Tabellen zu halten. Der Begriff kommt aus einer sehr allgemeinen Form des Programmbegriffs, es lohnt nicht, allzu viele Gedanken auf ihn zu verschwenden.

Dazu: Tabelle (Trellis)

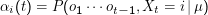
Dazu zählen wir die Zustände des HMM einfach irgendwie durch. Der Index i von α_i(t) ” durchläuft“ dann alle möglichen Zustände, der Parameter t die Zustandsfolge. Im fertigen Trellis stehen die Wahrscheinlichkeiten dafür, nach der Beobachtung von o₁o_t-1 zum Zeitpunkt t im Zustand i zu landen.

Aufbauen der Tabelle: α_i(1) = δ_ik mit k Index des Startzustands; von dort ” nach vorne“ (d.h. zu späteren Zuständen hin) durcharbeiten:

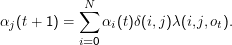
δ_ij ist das Kronecker-Symbol

so dass anfangs die Wahrscheinlichkeit für den Startzustand Eins ist, die für alle anderen Null. Dieses δ hat nichts mit unserer Übergangsfunktion δ zu tun!

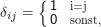
Danach werden einfach die Wahrscheinlichkeiten aller Übergänge, die auf den augenblicklichen Zustand führen können und dabei o_t emittieren, aufsummiert.

Ein Bild mag helfen; hier die Berechnung von α₂(t+ 1):

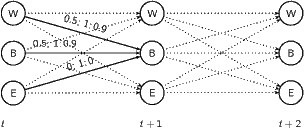
Sei α₁ (t) = 0.15, α₂(t) = 0.05, α₃(t) = 0.02. Wenn von t auf t+ 1 eine 1 emittiert wurde, ist

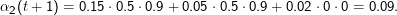
Die totale Wahrscheinlichkeit für die Beobachtung O ist dann

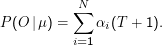
Wir berechnen hier also einfach die Summe der Wahrscheinlichkeiten, dass das Modell bei der gegebenen Ausgabe im Zustand i endet. Bei vielen Markow-Modellen werden ziemlich viele der α_i(T+ 1) null sein, z.B. für alle Zustände, die gar keine ankommenden Übergänge haben, die das letzte Zeichen emittieren.