Hidden Markov Models (HMMs) sind Markov-Ketten, in denen bei jedem Übergang etwas ausgegeben wird – was, wird wiederum von einer Wahrscheinlichkeitsverteilung bestimmt.
Allgemein: Ein HMM ist ein Tupel μ= (Φ,Σ,S,δ,λ). Dabei ist
- Φ eine Menge von Zuständen,
- Σ eine Menge von Ausgabesymbolen,
- S∈Φ ein Startzustand,
- δ:Φ →Φ ×[0,1] eine Menge von Verteilungen, die die Übergangswahrscheinlichkeiten für jeden Zustand beschreibt,
- λ:Φ ×Φ →Σ ×[0,1] eine Menge von Verteilungen, die zu jedem Übergang die Wahrscheinlichkeiten für die Ausgabe eines Zeichens bestimmt.
Die Funktionen λ und δ haben wir hier etwas komisch notiert. Das kommt daher, dass es Abbildungen von ” komischen“ Mengen (etwa der Menge aller Paare von Zuständen) in andere ” komische“ Mengen (etwa die Menge aller Verteilungen über den Ausgabesymbolen) sind. In der Realität werden wir δ(i,j) für die Übergangswahrscheinlichkeit von i nach j schreiben und λ(i,j,k) für die Wahrscheinlichkeit, dass bei diesem Übergang das Symbol k ausgegeben wird.
Es gibt viele Variationen zu diesem Thema, beginnend bei der Notation. Eine wichtige Variation ist, statt des Startsymbols S eine Verteilung Π auf Φ anzugeben, die die Wahrscheinlichkeiten angibt, dass das HMM in den jeweiligen Zuständen startet.
Manning und Schütze schreiben für unsere Übergangswahrscheinlichkeiten δ(X1,X2) ein aX1,X2 und für unsere Emissionswahrscheinlichkeiten λ(X1,X2,ot) ein bX1,X2,ot.
Außerdem könnte man statt arc emission (die Zeichen werden bei Übergängen geschrieben) auch state emission verwenden, bei der im Zustand geschrieben wird, nicht bei Übergängen. Dann wäre λ:Φ →Σ ×[0,1].
Diese und weitere Variationen ändern nur Details, die resultierenden HMMs haben alle die gleichen Fähigkeiten und Beschränkungen.
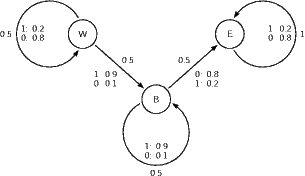
Darstellung eines HMM: Zustände als Kreise, Übergänge mit nichtverschwindender Wahrscheinlichkeit als Pfeile, die mit Übergangswahrscheinlichkeiten und der Verteilung der Ausgabesymbole gekennzeichnet sind.
Wichtig: HMMs können identische Sequenzen aus verschiedenen Zustandsfolgen generieren.
Das folgende HMM modelliert z.B. das Ergebnis der Übertragung eines senkrechten schwarzen Streifens durch einen verrauschten Kanal, der hin und wieder weiße (0) durch schwarze (1) Pixel ersetzt. Am Anfang werden (im Zustand W) mit hoher Wahrscheinlichkeit Nullen emittiert, dann kommt der Streifen (im Zustand B), wo mit hoher Wahrscheinlichkeit Einsen emittiert werden, und schließlich kommt weiß rechts vom Streifen im Zustand E.
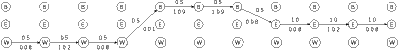
(1 ⋅0.8) ≈8.3 ×10-6. Es gibt aber viele weitere Wege durch das
Modell, die dieselbe Ausgabe erzeugen würden, die totale Wahrscheinlichkeit für diese spezielle Ausgabe ist also höher.