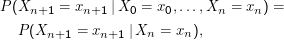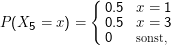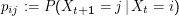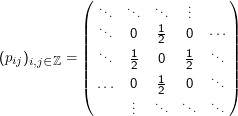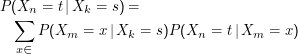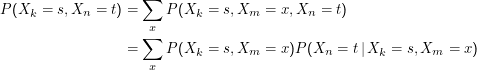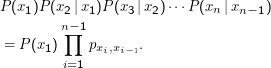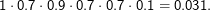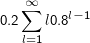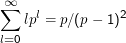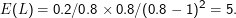27. Markow-Ketten
Sei T⊆ℕ eine Indexmenge (typisch: die Zeit, Position des Worts im
Text, Position des Phons), (Xt)t∈T eine Familie von Zufallsvariablen mit Werten in X. Dann heißt Xt stochastischer
Prozess.
Ein klassischer stochastischer Prozess ist die Brown’sche Bewegung (auch: Random Walk). In der einfachsten Version ist X dabei die
Position des Teilchens im (der Einfachheit halber eindimensionalen) Raum, t die Zeit. Bei jedem Schritt geht das Teilchen jeweils mit
Wahrscheinlichkeit 0.5 nach oben oder unten.
Für uns allerdings viel wichtiger ist die Interpretation eines Textes als stochastischer Prozess – wir hatten das bisher als ” Folge von
Zufallsvariablen“ gefasst, was eigentlich genau der stochastische Prozess ist. Da es uns jetzt aber verstärkt um Abhängigkeiten der Xt
untereinander gehen soll (während wir bisher immer die i.i.d.-Annahme hatten), wollen wir die Begriffe etwas genauer
definieren.
Eine Markow-Kette ist ein stochastischer Prozess, bei dem gilt:
wenn
die Bedingung überhaupt erfüllbar ist.
Das bedeutet zunächst nichts weiter, als dass Xn+1 nur von Xn bestimmt wird, das Verhalten des Systems also nur vom
vorhergehenden Zustand abhängig ist. Die Brown’sche Bewegung ist so ein Fall: Wenn wir wissen, dass X4 = 2, so ist die Verteilung
von X5
ganz
egal, was
X0,…,X3 sind.
Markow wird in der englischen Literatur üblicherweise Markov geschrieben (historische Anmerkung: Die erste Markow-Kette, die in der
Literatur verzeichnet ist, beschrieb die Abfolge der Zustände ” Konsonant“ und ” Vokal“ in russischer Literatur und sollte eigentlich
dazu dienen, die Notwendigkeit der Unabhängigkeit für das Gesetz der großen Zahlen nachzuweisen).
Eine Markow-Kette heißt stationär oder homogen, wenn für alle i,j∈X die Übergangswahrscheinlichkeit
unabhänging von
t ist.
Dies bedeutet, dass nicht nur die Geschichte keine Rolle für die Übergangswahrscheinlichkeiten spielt, sondern dass noch dazu auch die
Zeit unwichtig ist. Die Brown’sche Bewegung ist homogen.
Homogene Markow-Ketten lassen sich offenbar allein durch die Zahlen pij charakterisieren, also einfach alle Übergangswahrscheinlichkeiten
(bei nicht-homogenen Markow-Ketten wären die pij Funktionen und keine Zahlen). Wir haben damit schlimmstenfalls
abzählbar unendlich viele Zahlen, die durch zwei Indizes organisiert sind, also eine Matrix. Diese spezielle Matrix heißt
Übergangsmatrix.
Die Übergangsmatrix der Brown’schen Bewegung ist
Eine Übergangsmatrix ist ein Beispiel für eine stochastische Matrix. Da in solch einer Matrix zeilenweise Wahrscheinlichkeiten stehen,
muss für ihre Koeffizienten pij gelten:
Stochastische Prozesse in der Computerlinguistik sind in aller Regel stationäre Markow-Ketten, die Werte der Zufallszahlen als
”Zustände“ interpretierbar. Unsere Markow-Ketten sind meist endlich lang, während man sich im ” Mainstream“ gerne mit unendlichen
Ketten auseinandersetzt und z.B. nach Rekurrenz und Transienz von Zuständen oder Absorptionswahrscheinlichkeiten
fragt.
Dabei heißt ein Zustand x rekurrent, wenn der Zustand x mit Wahrscheinlichkeit 1 beliebig oft angenommen wird, transient sonst.
Eine Absorptionswahrscheinlichkeit entsteht, indem man eine Teilmenge J von X als ” absorbierend“ definiert, der Prozess also
abgebrochen wird, wenn das erste Xn einen Zustand aus J annimmt. Bei der Brown’schen Bewegung könnte das beispielsweise eine
Wand bei j sein, so dass der Prozess endet, sobald Xn < j wird. Die Frage ist nun, mit welcher Wahrscheinlichkeit der Prozess bei
bestimmten Anfangsbedingungen endet.
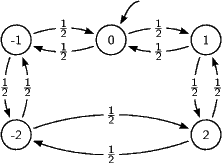
Graph einer Brown’schen Bewegung mit fünf Zuständen und periodischen Randbedingungen
Eine direkte Folge der Markow-Eigenschaft ist die Chapman-Kolmogorow-Gleichung
für alle
t, s∈
X und
k < m < n.
Das bedeutet, dass die Wahrscheinlichkeit, ” indirekt“ vom Zustand s (” Source“) zum Zustand t (” Target“) zu kommen, durch
Summieren über alle möglichen Zwischenwege berechenbar ist.
Zum Beweis nehmen wir zunächst speziell k= n+ 2 und m= n+ 1 an. Es ist
Wegen
der Markow-Eigenschaft ist
P(
Xn =
t|
Xk =
s,Xm =
x) =
P(
Xn =
t|
Xm =
x) (hier brauchen wir unsere spezielle
Annahme von oben). Eine Division durch
P(
Xk =
s) liefert die Behauptung für den Spezialfall. Die Verallgemeinerung folgt mit
vollständiger Induktion (was wir hier nicht machen, aber eine nette Übung ist).
Die Gesamtwahrscheinlichkeit für eine bestimmte Zustandsfolge P(x1,…,xn) ist einfach
Darin haben wir P(Xi = xi) als P(xi) abgekürzt.
Ein weiteres Beispiel für eine Markow-Kette ist folgenes Modell moderner Poesie:
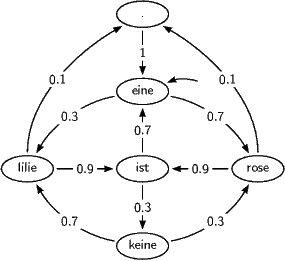
Der Startzustand ist dabei – wie üblich – durch einen Pfeil ohne Quellzustand markiert.
In ein Programm verwandelt, das jeweils die Namen der Zustände, durch die das Modell läuft, ausgibt, liefert es Sätze wie: ” eine rose
ist eine lilie ist eine rose ist eine lilie.“ oder ” eine rose.“ oder ” eine rose ist eine rose ist eine rose ist keine lilie ist keine
rose ist eine lilie ist eine rose ist keine rose ist keine rose ist eine lilie.“ Dabei wurde der ” .“-Zustand als absorbierend
definiert.
Die Wahrscheinlichkeit für den Satz ” eine rose ist eine rose.“ ist nach unseren Überlegungen oben
Exkurs: Page Rank
Der Page Rank ist eines der zentralen Ordnungskriterien für Suchergebnisse bei Google und interpretiert Links als Empfehlungen, rankt
also Seiten, auf die viele Links zeigen, hoch, wobei Links von Seiten mit hohem Page Rank wiederum als ” wertvoller“ gerechnet werden.
Brin und Page, die sich das ausgedacht haben, kamen eher aus der Algebra und berechneten die Page Ranks aus dem Eigenvektor zum
Eigenwert 1 der Matrix, die die Linkstruktur des Webs repräsentiert (eine wahrhaft große Matrix mit etlichen Milliarden Zeilen und
Spalten, wobei allerdings glücklicherweise die meisten Einträge Null sind, weil ja eine bestimmte Seite nur auf relativ wenig andere
Seiten verweist).
Eine alternative Interpretation des Page Rank ist aber die als die asympotitsche Aufenthaltswahrscheinlichkeit eines
”Random Surfers“, der auf irgendeiner Seite startet und dann immer einem zufälligen Link folgt. Das ist letztlich ein
Markow-Prozess, wobei natürlich ein paar Tricks gemacht werden müssen, damit die (hier nicht entwickelte) Mathematik greifen
kann (z.B. gibt es im Web Sackgassen, also Seiten ohne Links, die die Ergodizität dieses Prozesses kaputt machen).
Übungen zu diesem Abschnitt
Ihr solltet euch wenigstens an den rötlich unterlegten Aufgaben versuchen
(1)
Holt euch von der Webseite zur Vorlesung das Skript markovmodel.py. Seht euch darin die Klasse DistFunc an – mit ihr werden
wir nachher den jeweils nächsten Schritt ziehen. Sie wird mit einer Verteilung konstruiert (hier einfach eine Liste von
Zahlen). Ruft man draw() oft genug auf, sollten die Ergebnisse auf Dauer entsprechend der übergebenen Verteilung
verteilt sein. Könnt ihr sehen, wie das hier funktioniert? Probiert aus, ob das stimmt. Benutzt dafür Code, der etwa so
aussieht:
for val in DistFunc([1,1,1]).sampleRandomly(1000):
print val
Schickt die Ausgabe in einer Pipe durch sort | uniq -c – die Zahlen von 0 bis 2 sollten etwa gleich häufig vorkommen. Probiert
das auch mit anderen Verteilungen.
(2)
Verschafft euch einen groben Überblick über MarkovModel. Der Konstruktor des MarkovModels bekommt ein Dictionary-Literal in
einem String übergeben und baut daraus eine Listen von Listen, f, bei der in jeder Unterliste die Wahrscheinlichkeit für einen Übergang
vom Zustand index-der-unterliste in den Zustand index-in-der-liste steht. Das brauchen wir z.B. in computePathProb, um die
Wahrscheinlichkeit auszurechnen, dass eine bestimmte Zustandsfolge vom gegebenen Markov-Modell erzeugt wird. Daraus baut die
Klasse anschließend eine Liste von DistFuncs, mit der wir z.B. in driveOn den nächsten Zustand ziehen können.
(3)
Seht euch an, wie das Markov-Modell einen (periodischen) Random Walk durchführt. Benutzt dafür das Modell
{
0: {1:0.5,-1:0.5},
1: {0:0.5,2:0.5},
2: {1:0.5,-2:0.5},
-1: {-2:0.5,0:0.5},
-2: {-1:0.5,2:0.5},
}
– ihr könnt das in eine Datei schreiben und ihren Inhalt dann beim Konstruieren an das MarkovModelübergeben. Seht euch zunächst
ein paar kurze Zustandsfolgen an (vielleicht zehn Schritte lang), um ein Gefühl zu bekommen, was da so passiert. Erzeugt dann eine
lange Zustandsfolge (vielleicht 1000 Schritte lang) und lasst euch die Verteilung der Zustände innerhalb dieser Folge ausgeben – am
einfachsten geht das wieder mit den üblichen Unix-Tools durch
python markovmodel.py randomWalk.txt | sort | uniq -c
Verändert jetzt z.B. die 2 in der Zeile für den Zustand 1 in z.B. eine eins. Wie verändert sich die Verteilung der Zustände?
(4)
Lasst jetzt 100 Mal hintereinander ein zufällig aufgesetztes Markovmodell für zehn Schritte laufen und lasst euch
die summierte Verteilung der Zustandsfolgen ausgeben. Das geht z.B. mit folgendem Code und der Kommandozeile
oben
for i in xrange(100):
m.setUpUniform()
print "\n".join(map(str, m.getAPath(10)))
Auch hier sollte wieder eine Gleichverteilung herauskommen. Dies ist ein Spezialfall eines wichtigen Begriffs, nämlich der Ergodizität.
Im Groben sind Systeme ergodisch, wenn das Mittel einer Eigenschaft über ganz viele Kopien (Scharmittel) dem Mittel dieser
Eigenschaft über einen ganz langen Lauf eines Systems entspricht (Zeitmittel). Kurz: Zeitmittel=Scharmittel.
Die Ergodizität eines Markov-Modells ist sehr kritisch für seine einfache Trainierbarkeit. Im Allgemeinen sind Markov-Modelle, in
denen alle Zustände in alle übergehen können, ergodisch und damit harmlos.
(5)
Um ein einfaches Beispiel für nichtergodische Systeme zu haben, nehmt folgendes Markovmodell:
{
0: {1:0.5,-1:0.5},
1: {0:0.5,2:0.5},
2: {1:0.5,-2:0.5},
-1: {-2:0.5,0:0.5},
-2: {-2:1},
}
Wiederholt den Vergleich von Zeitmittel (eine lange Kette) zu Scharmittel (viele kurze Ketten) aus den letzten beiden Aufgaben. Woher
kommt das nichtergodische Verhalten?
(6)
Die MarkovModel-Klasse kann auch Fälle, in denen Zustände wirklich ” absorbierend“ sind in dem Sinn, dass eine Exception
ausgelöst wird, wenn das Modell in den betreffenden Zustand kommt. Nehmt folgende Übergangsverteilungen:
{
0: {0:0.5, 1:0.5,-1:0.5,-2:0.5,2:0.5},
1: {0:0.5, 1:0.5,-1:0.5,-2:0.5,2:0.5},
2: {0:0.5, 1:0.5,-1:0.5,-2:0.5,2:0.5},
-1: {0:0.5, 1:0.5,-1:0.5,-2:0.5,2:0.5},
-2: {},
}
– damit wir nachher leichter rechnen können, verlassen wir jetzt den Random Walk und lassen alles in alles übergehen (für die
Normierung sorgt nachher MarkovModel selbst). Wir interessieren und jetzt für die Lauflänge eines Markow-Modells, bis es in den
absorbierenden Zustand kommt. Das ist häufig eine interessante Frage (allerdings meines Wissens selten in der Sprachverarbeitung, ihre
Untersuchung ist aber für das Verständnis von Markowprozessen trotzdem hilfreich).
Diese Lauflänge L ist eine Zufallsvariable (über welchem Ω?). E(L) kann ganz gewöhnlich als ∑
l=1∞lP(L= l) ausgerechnet
werden. P(L= l) lässt sich am besten als Wahrscheinlichkeit auffassen, dass der Pfad bis l-1 nicht absorbiert wurde, das aber bei l
passiert.
Woher bekommen wir P(L= l)? Wegen der Gleichverteilung, die wir ” erzwungen“ haben, ist das hier nicht schwer.
Wir haben l-1 Schritte eine Wahrscheinlichkeit von 0.2 gehabt, absorbiert zu werden und haben das vermieden
(mithin mit Wahrscheinlichkeit 0.8) und sind beim l-ten Mal in die Falle getappt (wofür die Wahrscheinlichkeit 0.2
war).
Wir haben damit P(L= l) = 0.8l-1 ×0.2.
Im allgemeinen Fall ist das viel komplizierter – ihr könnt ja eine Weile grübeln, wie sowas mit dem Markovmodell aus der letzten
Aufgabe aussehen würde. Aber grübelt nicht so lang.
Jetzt können wir die Summe oben als
ausrechnen. Eine Formelsammlung verrät, dass
gilt.
Wenn wir ein 1
∕0
.8 ausklammern, können wir die Formel anwenden und erhalten
Prüft dieses Ergebnis empirisch nach: Mit dem obigen Automaten wirft driveOn eine Exception, wenn es im absorbierenden Zustand
landet. getAPath bricht dann die Generierung des Pfads ab, und die Länge des Pfades gibt gerade L. computeLExpect nutzt das
aus. Interessant bei der Sache ist auch, das Gesetz der großen Zahlen in Aktion zu sehen, wenn ihr mit ” großen Zahlen“ in die Zahl der
Experiment geht.
Wenn euch das näher interessiert: Man kann hier allerlei Statistiken darüber anstellen, welche Pfade wie häufig vorkommen. Das ist mit
unserem vereinfachten Modell langweilig, mit den nicht vollständig durchverbundenen Modellen oben aber recht spannend.
Dateien zu diesem Abschnitt
Markus Demleitner
Copyright Notice