Besser als der Naive Bayesian Classifier zumindest zur Spamerkennung ist der um Heuristiken angereicherte Plan for Spam von Paul Graham. Interessant ist dabei vor allem die Kombination von ” first principles“ und Einsichten über den Objektbereich. Ich werde hier nur ein paar grundsätzliche Punkte behandeln, mehr ist auf der oben zitierten Seite zu finden.
Nehmen wir zunächst an, wir wollten nur mit einem einzigen Wort w zwischen S und nicht S klassifizieren. Dann ist einfach
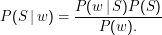
Um Entartungen zu vermeiden, legen wir außerdem fest, dass die größten und kleinsten Wahrscheinlichkeiten 0.99 und 0.01 sind und inferieren nur Wahrscheinlichkeiten für Wörter, die mehr als etwa 5 Mal im Gesamtkorpus vorkommen. Hier sehen wir wieder mal einen nicht-erwartungstreuen Schätzer. Tatsächlich würden wir hier ja vielleicht lieber mit Good-Turing anrücken – aber unser Klassifikationsproblem verträgt diese heuristische Vorschrift in der Tat besser als einen ordentlich begründeten Schätzer.
Wir wollen jetzt P(S|ω) aus mehreren Wörtern schätzen. Wir haben weiter die Naive Bayesian Assumption, müssen also nur ∏ w∈ωP(w|S) multiplizieren.
Es fehlen noch der Prior und die Normalisierung. Als Prior verwenden wir P(H) = P(S) = 0.5. Das mag willkürlich wirken, aber die Annahme von Gleichverteilung gilt gemeinhin als harmlos. Könnten wir uns auf unseren Korpus in dem Sinn verlassen, dass er tatsächlich aus dem ” typischen“ Mailaufkommen gezogen ist, also so viel Spam und Ham enthält wie eben an Mail reinkommt, könnten wir die Frequenzen im Korpus verwenden. Wirklich schlau wäre das aber nicht, weil dies viele in Wirklichkeit wichtige Parameter verdecken würde. Wenigstens in Europa kommt z.B. der größte Teil des Spam über Nacht an, man bräuchte also zeitabhängige Prioren. Allerdings stellt sich heraus, dass der Prior im Groben unwichtig ist und nur bei verschwindend wenigen Mails seine (vernünftige) Wahl einen Einfluss auf die Entscheidung hätte.
Die Normalisierung ist auch hier im Prinzip nicht nötig, aber es ist toller, wenn man eine Mail mit einer Wahrscheinlichkeit von 0.99 oder 0.71 als Spam klassifizieren kann.
Die Normalisierung könnten wir durch die volle Bayes-Formel machen (Division durch P(w)), einfacher aber ist es, P(S|ω) und P(H|ω) zu berechnen und durch die Summe zu teilen – wir wissen, dass P(c|ω) normalisiert sein muss.
Zusammen ergibt sich:
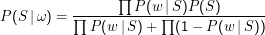
Das Ganze funktioniert noch erheblich besser, wenn man nur die N ” signifikantesten“ Wörter verwendet, d.h. die mit den größten Abweichungen vom ” neutralen“ 0.5. Graham empfiehlt N= 15. Dies beugt auch Numerikproblemen vor.