25. Bayesianische Klassifikation

Ziel der Klassifikation ist, bestimmte Versuchsausgänge einer von potenziell vielen Klassen zuzuordnen. Beispiele wären: Artikel in Klassen wie ” Klatsch“, ” Politik“, ” Feuilleton“ einteilen, Mails in Spam oder Ham, Spektren in verschiedene Stern- oder Galaxiensorten, Betriebszustände in normal, kritisch und ” Good Bye, Heidelberg“ und so weiter.

Formal wir haben Klassen v_j ∈V und ” Trainingsdaten“ D⊂Ω ×V (also Paare von Beobachtungen und gewünschten Klassen, z.B. (Artikel1, Klatsch), (Artikel2, Politik) usf.). Wir haben weiter Hypothesen h_i ∈H, deren jede eine Verteilung P(v_j,ω|h_i) gibt (also letztlich sagt, zu welcher Klasse v_j ein ω gehören soll). Die bayes-optimale Klassfikation eines Ergebnisses ω ist dann

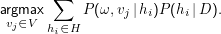
Im Groben addieren wir also für jedes v_j einfach die von allen Hypothesen h_i ausgespuckten Wahrscheinlichkeiten, dass ω von der Klassev_j ist mal die Wahrscheinlichkeit der Hypothese selbst unter den gegenbenen Trainingsdaten – diese Rechnung ist richtig, weil die Ereignisse ” v_j ist die korrekte Klassifikation“ disjunkt sind.

Bei nur zwei Hypothesen ist das Ergebnis des Klassifizierers natürlich das Gleiche, als hätte man zunächst die MAP-Hypothese bestimmt und dann nach dieser klassifiziert. Schon bei drei Hypothesen kann das aber anders sein. Sei etwa P(h_1,2,3 |D) = 0.4,0.3,0.3. Wir könnten nun für ein ω etwas wie P(1,ω|h₁) = 1 und P(0,ω|h₂) = P(0,ω|h₃) = 1 haben, d.h. die Hypothese h₁ klassifiziert sicher als 1, die beiden anderen sicher nach 0. Die MAP-Hypothese ist damit h₁, die danach wahrscheinlichste Klassifikation also 1. Unser Bayes-optimaler Klassifzierer würde hingegen

also 0 vorhersagen.

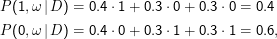
Man kann zeigen, dass es für einen gegebenen Hypothesenraum und gegebene Trainingsdaten keinen im Mittel besseren Klassifizierer gibt, dass also kein anderes Verfahren ” meistens“ bessere Ergebnisse liefert.

Leider ist der Bayes-Optimale Klassifizierer – wie eigentlich die meisten ” optimalen“ Verfahren in der Regel völlig unpraktikabel, weil – jedenfalls ohne weitere Annahmen – H gigantisch sein sollte (versucht, einen Hypothesenraum zur wortbasierten Klassifikation von Dokumenten in Dokumentenklassen zu bestimmen) und damit die Summe nicht realistisch berechenbar ist, von den Problemen, die P(h_i |D) schätzen, ganz zu schweigen.

Naive Bayesian

Unser typisches Klassifikationsproblem ist die Zuordnung einer Sammlung von Werten x= ⟨a₁,…,a_n⟩ zu einer Klasse v∈V. Diese Werte können etwa alle word tokens in einem Dokument sein oder die word tokens, die in der Umgebung eines bestimmten word types vorkommen.

Zur Klassifikation müssen wir lediglich

ausrechnen. Wir haben hier die Notation etwas vereinfacht – wenn wir nämlich unsere Hypothesen so wählen, dass die Hypothese h_i alles als v_i klassifiziert, können wir Hypothesen und Klassen identifizieren. Formal sagen wir P(v_j|h_i) = δ_ij. Dann sagt die Bayes-Optimale Klassifikation die Klasse voraus. Dabei haben wir im ersten Schritt P(a,b|c) = P(a|b,c)P(b|c) ausgenutzt (das folgt aus der Definition von bedingter Wahrscheinlichkeit, wenn man wieder bedenkt, dass ” ,“ hier einfach der Schnitt ist), im zweiten Schritt unsere Beziehung für P(v_j|h_i) eingesetzt, und schließlich die Eigenschaft des Kronecker-Delta, dass ∑ _ijδ_ij = j ist, ausgenutzt sowie freihändig P(h_i|D) = P(v_i|D) geschrieben, was aber wegen der Identifikation von vs und hs harmlos ist.

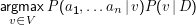
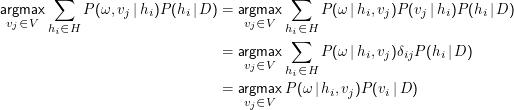
Diese Vereinfachung hilft noch nicht viel: Schon, wenn die a_i aus kleinen Mengen kommen, gibt es furchtbar viele a₁ , … , a_n. Nehmen wir etwa an, wir hätten 10 Klassen und wollten auf der Basis von 1000 Wörtern klassifizieren. Außerdem sehen wir nur auf Vorkommen von Wörtern (und nicht auf ihre Frequenzen), so dass wir eben 1000 a_i haben, die die Werte 0 oder 1 annehmen können. Wie viele Werte von P(a₁,…,a_n|v) müssen wir schätzen? Das Urnenmodell (hier haben wir ” Ziehung von 1000 Kugeln aus 2 mit Zurücklegen und mit Anordnung, also den Fall I) sagt uns, dass wir pro Klasse 1000² und mithin insgesamt 10⁷ Parameter schätzen müssten. Das sind furchtbar viele. Deshalb:

Naive Bayesian Assumption:

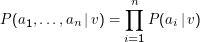
Das heißt nichts anderes, als dass das Auftreten des Attributs a_i von dem des Attributs a_j unabhängig ist. Das ist für unsere typischen Aufgaben grober Unfug, wie schon unser Beispiel mit Bundeskanzler und Schröder bei der Unabhängigkeit gezeigt hat. Trotzdem funktioniert der Naive Bayesian Classifier

häufig erstaunlich gut.

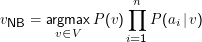
Hier reicht zum Training die Schätzung der n|V| Parameter P(a_i|v).

Als Beispiel mag das Filtern von Spam dienen. V besteht dann aus den beiden Klassen Ham (Mails, die wir bekommen möchten) und Spam (also unerwünschte Werbemail). Die Attribute können zunächst alle Wörter sein, die wir in den Mails vorfinden.

Wir brauchen also zwei Sammlungen von Spam und Ham (das D, sozusagen unser Korpus) und schätzen (ML tut es hier) die Verteilungen P(w|Spam) und P(w|Ham) für alle word types w, die wir in D finden. Kommt nun eine neue Mail ω, berechnen wir P(ω,Spam|D) und P(ω,Ham|D) – die Zahlen werden typischerweise sehr klein werden, es empfiehlt sich also, hier mit logarithmischen Wahrscheinlichkeiten zu operieren – und entscheiden uns für die wahrscheinlichere Klasse.

Das funktioniert, ist aber nicht so sonderlich gut, weil die Naive Bayesian Assumption von Mails und unseren Fragen an sie erheblich verletzt wird. Wie es etwas besser geht, steht auf der nächsten Folie.