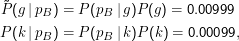24. Mehr Bayesianismus

Bayesian Updating

Wenn wir über eine Familie von Priors verfügen, können wir unseren Prior den Daten anpassen: Bayesian Updating. Idee dabei: nach jeder Beobachtung ω wird P_neu(μ_p) = P_alt(μ_p|ω).

Das geht mit diskreten Verteilungen als Prioren, was den Vorteil hat, dass man sich viel hässliche Mathematik erspart. Im folgenden Bild wurde von einer Gleichverteilung auf 28 Werten für p zwischen 0 und 1 ausgegangen und für 20 Bernoulli-Experimente mit p= 0.33 die Verteilung P(μ_p) per Bayesian Updating geschätzt.

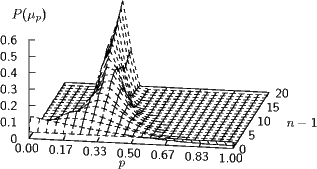
Will man wie im Beispiel den Parameter eines Bernoulli-Experiments schätzen, muss man nur P_neu(p) = b(n;N,p)P_alt(b) ausrechnen (die Zahl der Erfolge n kommt natürlich aus einem Experiment, z.B. einer wiederholten Auswertung eines Zufallszahlengenerators, die Zahl der ” Würfe“ N in einem Experiment ist im Prinzip frei wählbar, aber natürlich konvergiert der Schätzer schneller, wenn N größer ist) und das ausreichend lange iterieren.

Man kann nun die resultierenden Verteilungen so aufsummieren, dass ∑ _p=p1^p₂P(μ_p) >1 -α und hat so etwas wie einen Schätzer zum Niveau α. Das Intervall [p₁,p₂] entspricht dann in etwa unseren Konfidenzintervallen, aber nicht ganz, weshalb man diese Intervalle belief intervals nennt. Der Hit dabei ist, dass hier die ” natürliche“ Interpretation – wonach unser Parameter mit einer Wahrscheinlichkeit von 1 -α im Intervall liegt – richtig ist.

Bayes’sche Entscheidungen

Bayes hilft auch, Entscheidungen zwischen Hypothesen zu treffen. Eine Hypothese kann etwas sein wie p >0.3 bei einem Bernoulli-Experiment. In der Regel wird man aber eine ganze Menge von Hypothesen H= {h₁,h₂,...} haben, die dann etwas wie h₁ : 0 < p <0.2, h₂ : 0.2 < p <0.4 usf. sein könnten. In diesem Sinne ist die (diskrete) Schätztheorie ein Spezialfall des Entscheidens – allerdings werden wir uns beim Entscheiden nicht für Belief Intervals interessieren, sondern nur für die plausibelste Hypothese.

Gegeben sei eine Beobachtung D⊂Ω sowie ein Prior auf der Hypothesenmenge P(h). Die Hypothese gibt die Wahrscheinlichkeit für die Beobachtung von D. Wenn wir die wahrscheinlichste Hypothese suchen, müssen wir

berechnen.

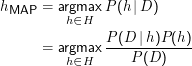
MAP steht hier für Maximum a posteriori.

Ein klassisches Beispiel kann wieder die medizinische Diagnostik sein. Anknüpfend an unser Burizystose-Beispiel von der bedingten Wahrscheinlichkeit wollen wir jetzt den Hypothesenraum H= {g,k} (für Gesund und Krank) untersuchen. Die Verbreitung der Krankheit in der Bevölkerung stellt sich hier als Prior dar, nämlich P(g) = 0.999 und P(k) = 0.001. Wir brauchen zur Berechnung noch die P(D|h).

Das Experiment läuft hier ab über Ω = {p_P,n_P}, nämlich dem positiven und negativen Ergebnis des Plutopharma-Tests. Nach der Problemstellung gilt

(natürlich müssen sich die bedingten Wahrscheinlichkeiten auch zu eins ergänzen, was formal einfach nachzuweisen ist, aber auch anschaulich klar ist: Egal, ob jemand krank oder gesund ist, fällt der Test auf jeden Fall positiv oder negativ aus).

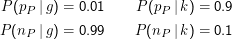
Wir rechnen jetzt den Posterior aus; P(D) müssen wir erstmal nicht ausrechnen, weil sich das nachher ohnehin aus der Normalisierung ergibt. Nehmen wir an, p_P tritt ein, der Test ist also positiv.

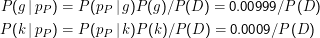
Nach Normalisierung ergibt sich:

– mithin ist die wahrscheinlichste Hypothese nach wie vor, dass der/die PatientIn gesund ist (klar, weil die Wahrscheinlichkeit, dass sie krank ist, eben so niedrig ist), aber unser Glaube an die Gesundheit ist angekratzt. P(D) hätte man hier natürlich auch direkt berechnen können als P(p_P|g) + P(p_P|k) = 0.01089 – der Weg über die Normalisierung ist aber in Anwendungen meistens bequemer.

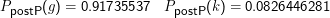
Meist muss P(D) aber gar nicht berechnet werden, denn es ist bei Variation von h konstant und spielt damit in der Berechnung von argmax keine Rolle.

Das Tolle an Bayesianischen Methoden ist nun, dass sie die Integration von Evidenz ermöglichen. Wir können nämlich nach diesem ersten, hoffentlich billigen Test, einen besseren und teureren machen, sagen wir die Buropsie. Für sie könnte

gelten. Wir können den Posterior aus der letzten Untersuchung als Prior der neuen verwenden und rechnen diesemal von vorneherein nichtnormalisiert; dabei soll der Test wieder positiv ausgefallen sein. Wir haben dann – also allen Grund, alarmiert zu sein, denn nun ist unsere MAP-Hypothese mit weitem Vorsprung k, in Worten krank.

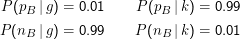
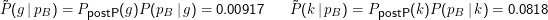
Beachtet, dass die zweite, die Nobeluntersuchung, alleine nicht zu diesem Schluss gereicht hätte. Setzt man den ursprünglichen Prior ein, ergibt sich hier

die MAP-Hypothese wäre also weiterhin ” gesund“