Bisher: Relative Häufigkeit im Zentrum der Überlegungen (” Frequentismus“). Alternative: Bayesianismus.
Es gibt hitzige Debatten zwischen Frequentisten und Bayesianern. Trotzdem sollte man keinen allzu großen Gegensatz konstruieren, korrekt eingeführte Wahrscheinlichkeiten und überlegte Anwendung der Methoden führen mit dem einen wie mit dem anderen Ansatz zu ” richtigen“ Ergebnissen. Allerdings hat der Bayesianismus gerade in der Computerlinguistik mit ihren häufig unbefriedigenden Daten und wenigstens teilweise durchaus vernünftig begründbaren Erwartungen einige Vorteile.
Grundidee ist, nicht zu glauben, es gebe eine richtige Hypothese und die Beobachtung auf diese Hypothese zu bedingen (Hintergrund von ML ist letztlich argmaxpP(o|μp)), sondern eher von der Beobachtung auszugehen und die Modelle auf diese Beobachtung zu bedingen, also etwa P(μp|o) zu betrachten.
Das ist zunächst grundvernünftig, denn immerhin wissen wir ja nur die Beobachtung mit Bestimmtheit – die Modelle kommen von uns, und auf sie zu bedingen heißt irgendwo, auf Phantasie zu bedingen. Aber das sollte nicht so ernst genommen werden, denn auch BayesianerInnen brauchen Modelle.
Viel dramatischer ist, dass Bayesianer eben auch Theorien oder Modellen ” Wahrscheinlichkeiten“ zuschreiben, und das ist es, was die Frequentisten ärgert – letztere argumentieren nämlich, Wahrscheinlichkeiten könnten nur aus beliebig oft wiederholbaren Experimenten kommen, und in so ein Bild passen Modelle nicht rein. Tatsächlich ist schon eine Aussage wie ” Die Regenwahrscheinlichkeit am nächsten Sonntag ist 30%“ für Frequentisten ein Graus, weil es eben nur einen nächsten Sonntag gibt (während die Regenwahrscheinlichkeit an Sonntagen in Ordnung wäre).
Als Nebeneffekt des mutigen Schritts, Wahrscheinlichkeiten so zu emanzipieren, können Bayesianer Theorien auch ohne Daten Wahrscheinlichkeiten zuordnen. Das klingt nach schwarzer Magie, ist aber häufig gut motivierbar. Occams Klinge ist beispielsweise ein uraltes und bewährtes Prinzip der Naturwissenschaften und sagt in etwa ” Wenn du die Wahl zwischen einem einfachen und einem komplizierten Modell hast, nimm das einfache, wenns irgend geht“. Für uns könnte sowas heißen: Bevorzuge ein Modell mit wenigen Parametern gegenüber einem mit vielen. Oder auch: Bevorzuge ein Modell ohne allzu wilde Annahmen gegenüber einem, das mehr Mut braucht.
Ein Modell ist wieder eine aus einer Familie von Verteilungen gewählte Verteilung. Für ein Bernoulli-Experiment mit n Versuchen wäre ein geeignetes Modell für die Zufallsvariable E ” Zahl der Erfolge“
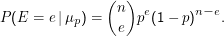
Ausgehend hiervon fragt der Frequentist nach dem Modell, das die Wahrscheinlichkeit der Beobachtung P(e|μp) maximiert. Wir das hatten in der Schätztheorie durch Betrachtung der Nullstellen der Ableitung (aus technischen Gründen der des Logarithmus) bestimmt:
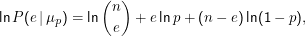
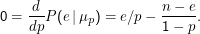
Letztlich sagt dies aber noch gar nichts – denn wir wissen, dass diese Antwort mit endlicher Wahrscheinlichkeit falsch ist. Um das handhaben zu können, hatten wir Konfidenzintervalle konstruiert, die so gemacht waren, dass wir die Wahrscheinlichkeit, unzutreffende Konfidenzintervalle zu erhalten, kontrollieren konnten, aber nicht in dem Sinn, dass die Fehlerwahrscheinlichkeit einer einzelnen Schätzung kontrollierbar war.
Wir möchten eigentlich lieber wissen, wie wahrscheinlich ein gegebenes Konfidenzintervall den konkreten Wert enthält:
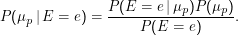
Problem: Was ist P(μp), was ist P(E= e)?
Die erste Frage bietet FrequentistInnen reichlich Gelegenheit zu Breitseiten: Kann man überhaupt Wahrscheinlichkeiten von Modellen definieren? (Nebenbei: Hier geht das natürlich unproblematisch, denn wir können mühelos eine Verteilung auf z.B. der Menge der Parameter Θ definieren – in allgemeineren Fällen, z.B. dem Wetter am nächsten Wochenende ist das nicht so unproblematisch) Und vor allem: Was sind vernünftige Annahmen für P(μp)?
Wenn wir P(μp) kennen, ist P(E= e) einfach, nämlich die Marginalwahrscheinlichkeit über alle möglichen Modelle – es ist nicht ganz verkehrt, sich das als Erwartungswert vorzustellen:
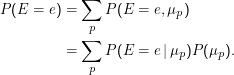
P(μp ) muss sozusagen a priori angenommen werden, daher heißt P(μp) auch Prior. Darin drückt sich dann eine Erwartung an das Modell aus; denkbar ist Gleichverteilung, Gleichverteilung über einem Intervall (Haar prior), Polynome, Gauss-Verteilungen usf.; diese Verteilungen lassen sich häufig streng ableiten oder wenigstens motivieren, ebenso häufig aber nicht.
Besonders nett sind so genannte non-informational Priors, deren Ziel ist, nicht mehr in die Beobachtungen reinzustecken, als wirklich drin ist. Die Gleichverteilung ist so ein Prior, oft nützlicher und erkenntnistheoretisch motiviert hingegen ist eine mathematische Umsetzung von Occams Klinge namens MDL, ausgeschrieben minimum description length.
Ausgehend davon können wir den für eine gegebene Beobachtung wahrscheinlichsten Parameter bestimmen als argmaxpP(μp).
Nehmen wir für P(μp) zunächst Gleichverteilung an. Dann gilt d∕dpP(μp) = 0, weiter ist hier ohnehin immer d∕dpP(E= e) = 0 (in der Summe oben wird das p wegsummiert, bevor das d∕dp es sehen könne – ähnliches gilt, wenn wir, wie hier eigentlich, mit kontinuierlichen Dichten arbeiten und statt Summen Integralzeichen hätten). Damit ist
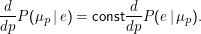
Nehmen wir aber an, wir hätten einen guten Grund, bestimmte Werte von p zu favorisieren. Für Bigramme beispielsweise haben wir gesehen, dass der Schluss von der Abwesenheit eines Bigramms im Korpus auf dessen Unmöglichkeit grober Unfug ist – und Bayesianismus lässt uns genau die Überzeugung, dass viele Bigramme eben doch möglich sind, obwohl wir sie nicht beobachten, in eine Theorie packen.
Der Einfachheit halber wollen wir im Beispiel daran glauben, dass p= 0.5 ein richtig guter Wert sei – sagen wir, für einen Münzwurf; die Beobachtung ist dann nach wie vor die Zahl der Erfolge e. Alle anderen (zwischen Null und Eins) sind aber auch irgendwie gut. Ein analytisch einfacher Prior in dieser Situation ist
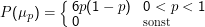
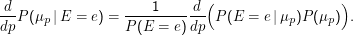
Wieder ist es technisch angenehemer, die Ableitung des Logarithmus auszurechnen – die Lage des Maximums verschiebt sich dadurch nicht. Die zu lösende Gleichung lautet dann
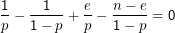
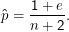
Interessant daran ist, dass dieser Schätzer mehr ” Trägheit“ hat als unser ML-Schätzer. Wenn wir 10 Erfolge in 10 Versuchen haben, sagt ML p= 1, unser Schätzer aber p= 11∕12. Das muss keine bessere Schätzung sein, erinnert aber daran, dass natürlich auch die fairste Münze mal nur Kopf liefern mag und eben nicht klar ist, dass Erfolg das sichere Ereignis ist. Ebenso gehen wir bei 0 Erfolgen nicht gleich auf p= 0 wie ML, sondern eben nur auf p= 1∕12, bei acht Erfolgen auf p= 0.75 statt auf p= 0.8. Wenn wir einen stärker gepeakten Prior genommen hätten, wären wir auch weniger weit zum ML-Resultat marschiert, hätten wir einen schwächer gepeakten Prior genommen, wären wir näher zum ML-Resultat gekommen. Darin steckt eine gewisse Beliebigkeit, aber wie gesagt: Häufig gibt es gute Gründe, sich für einen bestimmten Prior zu entscheiden.