22. Testtheorie II

Eine andere Anwendung des χ²-Tests ist der Vergleich von Texten: Sind zwei Texte aus dem gleichen Grundkorpus gezogen oder nicht?

Unsere Tabelle sieht jetzt so aus:

			|w∈C1|		|w∈C2|
	w= studis		292		24
	w= wurde		290		58
	w= heidelberg		290		84

Die Teststatistik bleibt unverändert, ist jetzt aber ein Maß für die ” Abweichung vom Dreisatz“ (d.h., idealerweise wäre für aus dem gleichen Korpus gezogene Texte das Verhältnis der Zahlen in beiden Spalten über alle Zeilen konstant).

Problematisch ist die Auswahl der Wörter, die in die Tabelle aufgenommen werden. Die häufigsten Wörter sind typischerweise nicht sehr korpusspezifisch (der, und, in… ), seltene Wörter stören den Test. Denkbar: stop words (also manueller Ausschluss insignifikanter Wörter, verbunden mit Auschluss seltener Wörter), Quantile (etwa: Die 5% häufigsten und die 85% seltensten Wörter werden ausgeschlossen).

Ein Beispiel: Zwei Texte aus dem UNiMUT aktuell (Artikel vor und nach dem 10.9.2001), Ua und Un, ein Satz von Pressemitteilungen des Pressesprechers des Rektors der Uni Heidelberg, P, ein Artikel aus der Schülerzeitung MSZ, MS, und der schon erwähnte 18. Brumaire (englisch), B.

Wir wählen jeweils alle Wörter, deren Erwartung in den beiden zu vergleichenden Texten >4 ist. Leider wird sich die Zahl dieser Wörter je nach Paar drastisch unterscheiden, was die Anwendung der Testtheorie erschwert. Wir wollen nur ein Gefühl für die Verschiedenheit der Texte bekommen und dividieren deshalb das V ² durch die Zahl der verwendeten Wörter (also etwa die Zahl der Freiheitsgrade). Da die kritischen Werte im χ²-Test nicht linear ansteigen, ist das nicht streng richtig.

Das Ergebnis, jeweils als Verschiedenheit von Ua:

Text	Un	MS	P	B
V 2	2.27	2.70	14.4	144

Es werden also sehr schön sowohl verschiedene Texttypen (SchülerInnen-, Studierendenpresse vs. Presseerklärungen von Rektoren) als auch verschiedene Sprachen (Deutsch vs. Englisch) unterschieden. Bei genauerer Ausführung des Tests allerdings wird man finden, dass ohne große Tricks (eher linguistischer Natur) alle verwendeten Texte zu fantastischen Signifikanzniveaus verschiedenen Korpora angehören. Das allerdings liegt zu guten Stücken daran, dass die Behauptung, wir hätten bei so einem Vergleich so viele Freiheitsgrade wie word types, grundfalsch ist. Die Frage, wie die Zahl der Freiheitsgrade wirklich bestimmt werden sollte, ist allerdings schon wieder viel komplizierter.

Likelihood-Quotienten-Tests

Hintergrund der meisten Tests ist der Likelihood-Quotient

Ein Test φ ist ein L.-Q.-Test, wenn mit einem bestimmten c∈ℝ die Hypothese für q(x) < c angenommen, für q(x) > c verworfen wird.

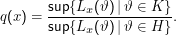
Der L.-Q. ist sozusagen das Verhältnis zwischen der Wahrscheinlichkeit der besten Erklärung für die Beobachtung von x, wenn die Alternative zutrifft und der Wahrscheinlichkeit der besten Erklärung, wenn die Hypothese zutrifft. Wenn letztere groß ist, ist q(x) klein, die Hypothese wird also angenommen.

Dass in der Formel das Supremum (sup) und nicht ein Maximum über die Menge der Werte der Likelihood-Funktion L_x für alle ϑ genommen wird, liegt daran, dass ϑ häufig reell sein wird, die Menge also überabzählbar sein kann. Solche Mengen müssen nicht unbedingt ein Maximum haben, selbst wenn sie beschränkt sind – die Menge M= {x²∕(x² -1)|x∈ℝ} etwa ist eine Teilmenge von [0,1], und sicher sind alle Elemente <1. Die Eins ist jedoch nicht in ihr enthalten. Umgekehrt gibt es zu jeder Zahl y <1 garantiert ein z∈M, so dass z > y, so dass 1 die kleinste Zahl ist, die jedes Element von M majorisiert. Das ist gerade das Supremum. Wem solche Subtilitäten zuwider sind, darf sich da ein Maximum vorstellen.

Sowohl der χ²- als auch t-Test sind L.-Q.-Tests, sie unterscheiden sich nach der Vorschrift, nach der c berechnet wird – wie das in einem relativ komplizierten Sinn optimal zu geschehen hat, hängt insbesondere von den zugrundeliegenden Verteilungen ab.

Der Likelihood-Quotient kann unter der Annahme, dass die Bigramme in der Tat binomialverteilt sind, für unser Kollokationsbeispiel recht einfach hingeschrieben werden – wir brauchen dann zunächst gar keine Annahmen mehr über irgendeine Sorte asymptotischen Verhaltens, wie sie für die Anwendbarkeit von t- und χ²-Test nötig sind. Dieses Verfahren ist in unseren Kreisen als Dunning’s Test bekannt.

Dazu formulieren zur Entscheidung, ob zwei Wörter x und y Kollokationen sind über unserem üblichen Bigrammodell folgende Hypothesen:

• H₁ – P(w₂ = y|w₁ = x) = p= P(w₂ = y|w₁≠y) (Unabhängigkeit, keine Kollokation)
• H₂ – P(w₂ = y|w₁ = x) = p₁≠p₂ = P(w₂ = y|w₁≠y) (Kollokation)

Jetzt schätzen wir die darin vorkommenden Wahrscheinlichkeiten per ML zu p= |y|∕N, p₁ = |xy|∕|x| und p₂ = (|y|-|xy|)∕(N-|x|).

Die wesentliche Annahme ist nun, dass die Frequenzen aus einer Binomialverteilung generiert werden, was im Wesentlichen heißt, dass die Bigramme unabhängig voneinander gezogen werden (auch diese Annahme ist natürlich falsch, aber nachweisbar ” weniger falsch“ als die, die hinter den anderen Tests stehen).

Man kann dann die Likelihoods der beiden Hypothesen berechnen; üblicherweise berechnet man gleich den Logarithmus des Verhältnisses, also

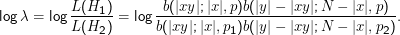
Man könnte jetzt auf die Idee kommen, sich für H₁ zu entscheiden, wenn dieses log λ größer als Null ist (weil dann das Verhältnis selbst größer als eins und mithin der Nenner größer als der Zähler ist).

Ohne weiteres wäre das fatal, weil die Hypothesen normalerweise nicht gleichberechtigt sind. In der Testtheorie hat man gerade deshalb Nullhypothese und Alternative eingeführt, und man möchte normalerweise schon ” starke Evidenz“ haben, um die Nullhypothese zu verwerfen – ” ein bisschen wahrscheinlicher“ reicht uns nicht. Dazu kommt, dass hier H₁ und H₂ nicht die gleiche Zahl freier Parameter haben – für H₁ kann man nur eine Zahl, p, wählen, für H₂ hat man zwei Zahlen. Es ist aber klar, dass ich eine gegebene Beobachtung immer werde besser beschreiben können, wenn ich mehr Parameter zur Anpassung meiner Theorie auf die Beobachtung habe. Man würde nun vielleicht gerne die Likelihood von H₂ irgendwie ” bestrafen“, um das auszugleichen – aber so etwas macht man besser in einem Bayesianischen Rahmen (vgl. unten). Dort heißt diese Sorte von Bestrafung MDL-Prior.

Im hier vorliegenden Fall arbeiten die beiden Effekte gegeneinander – die Nullhypothese der Unabhängigkeit wird zunächst immer wahrscheinlicher sein, weil sie nämlich zwei Parameter hat. Trotzdem hätte man gerne unsere mühsam erworbenen Instrumente (und vor allem das Niveau) auch hier. Tatsächlich ist das unter schwachen Annahmen möglich, denn die Größe -2log λ ist wieder asymptotisch χ²-verteilt, kann also als eine robustere Teststatistik in einem χ²-Test dienen.

Dunnings Test ist generell besser für unsere Probleme als der normale, auf Kontingenztabellen basierende χ²-Test. Trotzdem bleibt die Verwendung von -2log λ ein asymptotisches Resultat, Wunder bei praktisch nicht vorhandenen Daten darf mensch also auch nicht erwarten. An der Einsicht, dass man nur aus Daten schätzen kann, die man auch wirklich hat, führt bei aller Testtheorie eben kein Weg vorbei.