21. Identifikation von Kollokationen

Wir definieren P(w) als die Wahrscheinlichkeit, dass das Wort w auftaucht, P(w₁w₂) als die Wahrscheinlichkeit, dass w₂ hinter w₁ steht. Eine Formalisierung der Nullhypothese ” w₁ und w₂ stehen nicht besonders häufig nacheinander“ könnte sein P(w₁ w₂) = P(w₁)P(w₂).

Sehen wir, ob in unserem Brumaire-Text ” Louis Bonaparte“ überhäufig ist (d.h., wir nehmen an, die ML-Schätzungen der Worthäufigkeiten aus den Zählungen in dem Text gäben ein brauchbares Wahrscheinlichkeitsmaß – was eigentlich Unsinn ist, aber für ein Beispiel taugt). Der Brumaire-Text enthält mit einem naiven Tokenisierer 42570 Wörter und aus Wortzählungen folgt

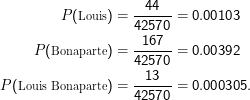
Damit haben wir 0.00103 ⋅0.00392 = 4.04 ×10^-6 als Schätzung für die Wahrscheinlichkeit von ” Louis Bonaparte“ unter Annahme der Unabhängigkeit der beiden Wörter, was mit der tatsächlich beobachteten Wahrscheinlichkeit von 3.09 ×10^-4 zu vergleichen ist. Offenbar sind die Werte verschieden (was natürlich nicht überrascht). Reicht aber die Verschiedenheit, um auf eine Überhäufigkeit des Bigramms (und damit auf eine Kollokation in unserem Sinn) zu schließen?

Nehmen wir ” party“ und ” you“ als Beispiel für ein Wortpaar, das sicher über jedem Kollokationsverdacht steht:

Es ist P(party)P(you) = 6.63 ×10^-6. Es scheint, als sei auch ” party you“ deutlich überhäufig. Es ist aber jedenfalls mal ” weniger überhäufig“.

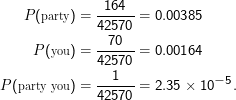
Wenden wir also unsere Testtheorie an, im Wissen, dass unsere Stichprobe so klein ist, dass wir uns hart am Rand des zulässigen befinden und darüber hinaus natürlich auch unsere ML-Schätzungen wenig Wert haben.

Häufig wird zur Klärung solcher Fragen der t-Test angewandt. Dabei hat man N normalverteilte Zufallsvariablen X_i . Zu testen ist, ob ein gegebener Erwartungswert μ₀ der Stichprobe entspricht oder nicht. Die Teststatistik ist dann

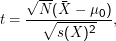
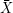worin und s(X)² unsere Schätzer für Erwartungswert und Standardabweichung sind.

Mit der Teststatistik geht man in eine Tabelle, die zu einem gegebenen N und α den kritischen Wert liefert.

Anwendung auf unser Beispiel: Die X_i sind definiert über einem Ω aller möglichen Bigramme, so dass X_i = 1, wenn das gesuchte Bigramm auftaucht und X_i = 0 sonst (man nennt ein X_i dieser Art auch gern Indikatorvariable für das Ereignis ” gesuchtes Bigramm gefunden“). Dies ist effektiv ein Bernoulliexperiment, das, wenn Louis und Bonaparte unkorrelliert wären, gerade mit p= 4.04 ×10^-6 verteilt sein müsste und entsprechend auch μ₀ = 4.04 ×10^-6 haben sollte – das jedenfalls ergibt die beste Annäherung durch eine Normalverteilung, die bei diesem p allerdings garantiert nicht atemberaubend gut sein wird. Weiter ist 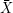= 0.000305 (nämlich die beobachtete Häufigkeit von ” Louis Bonaparte“), N= 42570 (genau genommen hätte das letzte Wort keinen Partner fürs Bigramm, es gibt also ein Bigramm weniger als es Wörter gibt), und unser Schätzer für s² ergibt

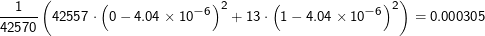
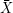(Übung: Macht euch klar, warum und s(X)² hier so nahe beieinanderliegen).

Unsere Teststatistik berechnet sich damit zu t= 3.56; wenn wir zu einem Niveau von α= 0.05 bestimmen wollen, dass Louis Bonaparte hier eine Kollokation darstellt, müssen wir laut Tabelle (vgl. fast beliebige Tabellenwerke, etwa auch am Ende von Manning-Schütze) über 1.645 kommen. Wir nehmen damit in Kauf, dass wir uns unter zwanzig Vermutungen einen Fehler erster Art machen. Das ist angesichts der sonstigen Unwägbarkeiten (die X_i sind sicher nicht unabhängig, und normalverteilt sind sie auch nicht – Fehler dritter Art) gar nicht schlecht. Wir können also die Nullhypothese der Unabhängigkeit von Louis und Bonaparte zum Niveau von 0.05 zurückweisen.

Wenn wir die gleiche Prozedur für ” party you“ durchziehen (tut es!), kommen wir auf eine Teststatistik von t= 0.71, was deutlich unter der Grenze von 1.645 liegt und uns nicht erlaubt, die Nullhypothese zu verwerfen.

Der t-Test unterstellt, dass X normalverteilt ist. Für unsere Zufallsvariablen gilt das fast nie. Deshalb populärerer Test: χ²-Test. Unter diesem Namen firmieren etliche verwandte Verfahren. Wir behandeln hier nur den Test auf Unabhängigkeit. Ihnen gemeinsam ist, dass sie schwächere Annahmen über die beteiligten Zufallsvariablen machen als der t-Test.

Idee: Vergleiche die Zahl der erwarteten Fälle mit der der beobachteten Fälle, so dass das die Teststatistik groß wird, wenn die Abweichungen von der Erwartung groß werden. Dazu Tabelle der Zahl der Bigramme w₁w₂ mit

			w1 = L.		w1≠L.
	w2 = B.		13		154		167
	w2 ≠B.		31		42372		42403
			44		42426		42570

Die Teststatistik ist

wobei O_i,j den beobachteten Wert in der i-ten Zeile und der j-ten Spalte und E_i,j den erwarteten Wert an dieser Stelle bezeichnen. Die E_i,j berechnen wir aus der Marginal” verteilung“.

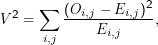
Dies entspricht einem ML-Schätzer. So ist E_1,1 einfach das Produkt der ML-Wahrscheinlichkeiten ganz unten in der ersten Spalte und ganz rechts in der ersten Zeile, wieder zurückgewandelt in eine absolute Häufigkeit,

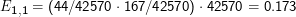
Die komplette Teststatistik ist, nach dieser Systematik berechnet, V ² = 958. Was bedeutet das? Zunächst nicht viel, unter bestimmten Umständen (die hier übrigens eigentlich nicht erfüllt sind, siehe unten) kann man aber annehmen, dass V ² einer χ_n²-Verteilung folgt (die Details sind da irrelevant, n ist jedoch die Zahl der Freiheitsgrade, in einer N×M-dimensionalen Tabelle ist das (N-1)(M-1)). Wenn das so ist, kann man in einer Tabelle nachsehen und finden, dass in unserem Fall der kritische Wert für V ² zum Niveau 0.05 bei gerade mal 3.84 liegt, wir haben also wieder gefunden, dass die Nullhypothese, Louis und Bonaparte seien unkorreliert, nicht angenommen werden kann (bzw. zurückgewiesen wird).

Für ” party“ und ” you“ sieht unsere Tabelle so aus:

			w1 = p.		w1≠p.
	w2 = y.		1		163		164
	w2 ≠y.		69		42337		42406
			70		42500		42570

Damit folgt ein V ² = 1.99 – auch der χ²-Test findet, dass die Nullhypothese der Unabhängigkeit für ” party you“ nicht verworfen werden kann.

Allerdings haben wir bei allen Untersuchungen an dem kleinen Brumaire-Text einen Fehler dritter Art gemacht, wir haben nämlich an zu wenig Daten gearbeitet, als dass wir den Tests ernsthaft Vertrauen entgegenbringen könnten.

Im Fall des χ²-Tests gibt es eine gute Faustregel, ab wann die Test wohl vertrauenswürdig sein werden: Wenn eine Erwartungszelle eine Zahl ≤2 enthält, ist der Test nicht mehr ” gut“, und man sollte sich etwas anderes Ausdenken. Hat man viele Freiheitsgrade, etwa n >10, mag auch eine Grenze von 1 für die Erwartungen ausreichen.

Wirklich überzubewerten ist das alles nicht – all die vorberechneten Tests machen Annahmen über Verteilungen, die den Beobachtungen zugrunde liegen, und diese Annahmen sind im Bereich der Sprachverarbeitung eigentlich immer verletzt. Eine genauere Untersuchung dieser Fragen findet sich etwa in Pedersen, Kayaalp und Bruce (1996).