Bei einem Test geht es darum, eine Hypothese zu prüfen, etwa, dass ” Bundeskanzler“ und ” Schröder“ eine Kollokation (in unserem Sinn) bilden.
Formal: Wir haben die Wertemenge X einer Zufallsvariablen X und eine Menge {Pϑ|ϑ∈Θ} von möglichen Verteilungen von X. Die Hypothese H⊂Θ ist eine echte Teilmenge von Θ, ihr Komplement K= Θ \H heißt Alternative. Der Test ist eine Vorschrift, ob ϑ∈H oder nicht. Im ersten Fall spricht man von der Annahme der Hypothese, im zweiten Fall vom Verwerfen.
Wie schon in der Schätztheorie wird jedem x∈X ein ϑ∈Θ zugeordnet. In ” fertigen“ Tests will man in der Regel das ϑ nicht mehr sehen und gibt deshalb lieber eine Menge R⊂X an, für die die Hypothese verworfen wird (den kritischen Bereich oder Verwerfungsbereich).
Wenn X⊂ℝ (das wird praktisch immer so sein), so wird R häufig durch eine Funktion T beschrieben, so dass R= {x∈ℝ |T(x) ≥t}. Die Funktion T heißt Teststatistik, die Zahl t ist eine vom Test abhängige Funktion des gewünschten Niveaus, die man sich entweder vom Computer ausrechnen lässt oder aus einer Tabelle abliest.
Ein Fehler erster Art liegt vor, wenn die Hypothese verworfen wird, obwohl sie richtig ist, ein Fehler zweiter Art, wenn die Hypothese angenommen wird, obwohl sie falsch ist, ein Fehler dritter Art, wenn das Modell falsch war.
Die Gütefunktion
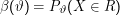
Warum ist das so? Nun, wenn ϑ∈H, dann sagt X∈R, dass die Hypothese verworfen wird, obwohl sie wahr ist – das ist der Fehler erster Art. Ist aber ϑ∈K, ist X∈R gerade das, was idealerweise herauskommen sollte; falsch liegen wir, wenn wir das Gegenteil entscheiden, die Fehlerwahrscheinlichkeit (für einen Fehler zweiter Art) ist dann also 1 -P(X∈R).
Grundsätzlich ist diese Formel der Schlüssel zum Verständnis der Aussage von Tests. Zur Verdeutlichung mag die folgende Grafik dienen:
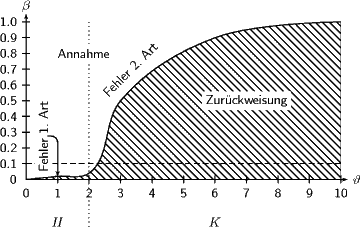
Hier ist ein (erfundenes) β(ϑ) geplottet. Im schraffierten Bereich wird zurückgewiesen (er gibt nach Definition von β für jedes ϑ die Wahrscheinlichkeit der Zurückweisung der Hypothese), im weißen Bereich angenommen. Links von der vertikalen gepunkteten Linie ist die Hypothese, rechts die Alternative (es ist durchaus denkbar, eine kompliziertere Topologie zu haben, etwa eine Hypothese, die auf beiden Seiten von der Alternative eingeschlossen ist – man würde dann von einem zweiseitigen Test sprechen). Demnach entspricht der schraffierte Bereich über H dem Fehler erster Art, der weiße Bereich über K dem Fehler zweiter Art.
Man ahnt auch, dass man in der Regel (und jedenfalls nicht bei kontinuierlichem ϑ und stetigem β) nicht gleichzeitig global Macht und Niveau kontrollieren kann – will man mehr Niveau, sinkt die Macht und umgekehrt. In der Praxis kontrolliert man eben den Fehler erster Art. Im Beispiel bleibt βüber H immer unter 0.1 (die gestrichelte waagrechte Linie), und so haben wir hier einen Test zum Niveau 0.1 (tatsächlich sogar zum Niveau 0.075, aber auch zu 0.4 usf.
Weil wir das Niveau kontrollieren und nicht die Macht, müssen wir unsere Tests so konstruieren, dass uns Fehler 2. Art nicht sehr jucken: Formulieren einer Nullhypothese H0, die das ” Un-überraschende“ behauptet: Gleichverteilung, Unabhängigkeit etc. Danach muss man nur noch die Teststatistik berechnen, Grenze zu Niveau aus Tabelle oder Programm ablesen.
Eine typische Wahl des Niveaus ist α= 0.05 (dahinter steckt nicht viel Weisheit – es ist einfach ein Kompromiss, auf den man sich in vielen Disziplinen geeinigt hat). Das bedeutet insbesondere: Wir müssen damit rechnen, dass eine von zwanzig Zurückweisungen der Nullhypothese fehlerhaft ist.
Dass die Macht eines Tests nicht global kontrollierbar ist, heißt nicht, dass nicht auch sie eine nützliche Größe wäre. Häufig ist es nämlich so, dass man gerne Effekte einer bestimmten Größe ausschließen möchte. Um das zu illustrieren, möchte ich kurz den Klassiker der Testtheorie seit den fundamentalen Werken von Fisher, Pearson und Neyman in der ersten Hälfte des 20. Jahrhunderts einführen:
Die Tea Testing Lady
Eine etwas schrullige Landadelige aus den Südwesten Englands behauptet, sie könne genau schmecken, ob bei ihrem Tee zunächst die Milch (wir sind in England – Tee ohne Milch zu trinken, kommt natürlich nicht in Frage) oder zuerst der Tee eingegossen wurde. Das klappt selbstverständlich nicht immer, aber doch meistens.
Um jetzt zu prüfen, ob diese Behauptung besser in eine Kategorie mit Schlossgespenstern und freier Marktwirtschaft zu stecken oder ob vielleicht doch etwas dran sei, kann man die Lady einfach etliche Tassen klassifizieren lassen und sehen, wie viel Erfolg sie hat. Wenn es egal ist, was zuerst in die Tasse kommt, sollten ihre Erfolge zufällig kommen, und zwar mit einer Erfolgswahrscheinlichkeit von 0.5. Nimmt man an, dass die einzelnen Versuche unabhängig voneinander sind, so müsste die Zahl ihrer Erfolge binomialverteilt sein.
Die Nullhypothese ist das, was die Lady gern widerlegen würde: p= 0.5. Die Alternative ergibt sich dann als p >0.5, dass nämlich die Lady öfter als durch reinen Zufall bestimmt richtig liegt. Den Fall p <0.5 ignorieren wir – formal könnten wir Θ = [0.5,1] setzen.
Wenn ihr nun die Aufgaben bearbeitet, findet ihr, dass ein Test mit 20 Versuchen und der Zahl der Erfolge als Teststatistik mit einem kritischen Wert von 15 noch ein Niveau von 0.05 hat (genauer sogar 0.02). Ihr seht allerdings auch, dass der Test ziemlich unfair gegenüber der Lady ist, weil beispielsweise β(0.7) auch nur gut 0.4 ist, wir also nur in gut 40% der Fälle die Nullhypothese zurückweisen würden, wenn die Lady immerhin 70% der Tassen richtig klassifizieren würde – was sicher als deutlicher Hinweis auf Forschungsbedarf zu werten wäre. Hier ist also die Macht des Tests nicht ausreichend.
Man kann nun die Macht des Tests einfach durch Verschiebung des kritischen Werts erhöhen – mit t= 12 etwa würden wir die Nullhypothese bei einer p= 0.7-Lady zu fast 90% zurückweisen und mithin glauben, dass etwas an ihrer Behauptung dran ist. Leider geht dabei das Niveau vor die Hunde, und wir würden mit einer Wahrscheinlichkeit von fast einem Drittel Scharlataninnen für Feinschmeckerinnen halten.
Der einzige Weg, das Niveau zu halten und die Macht zu erhöhen ist, die Fallzahl hochzupumpen. Mit einer Fallzahl von 80 und einem kritischen Wert von 49 haben wir immer noch ein Niveau von 0.05, haben aber unsere Macht bei p= 0.7 auf über 0.95 gesteigert.
Bei realen Testdesigns fragt man darum häufig: Wie viele Fälle brauche ich, um einen bestimmte Effektgröße noch mit einer bestimmten Macht behandeln zu können. Fertig gepackte Tests kommen häufig mit Vorschriften zur Berechnung von Fallzahlen.