10. Relationen II

Die inverse Relation R^-1 entsteht durch Vertauschung von Definitions- und Wertebereich und der Tupelelemente:

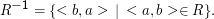
Davon wohl zu unterscheiden ist das Komplement einer Relation R⊆M×N, nämlich 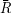= (M×N) \R.

Beispiel 1: M= {1,2,3}, R⊂M×M. Relation “ist kleiner als” ist R= {< 1,2 >,< 1,3 >,< 2,3 >}. 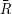ist dann “ist nicht kleiner als” oder “ist größer oder gleich”, R^-1 “ist größer als”.

Beispiel 2 (gilt nur für katholische Gegenden): Die Relation R, “ist Ehemann von” mit Männern als Wertebereich. 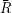ist die Relation “ist nicht verheiratet mit”, R^-1 ist dagegen “ist Ehefrau von” auf der Menge der Frauen.

Äquivalenzrelation

R⊆M×M heißt Äquivalenzrelation, wenn sie reflexiv, symmetrisch und transitiv ist.

Eine Äquivalenzrelation teilt eine Menge in Äquivalenzklassen (disjunkte Teilmengen, deren Vereinigung die Menge ist) ein.

Beispiel 1: Sei M die Menge aller deutschen Wörter. Die Relation

ist eine Äquivalenzrelation.

Beispiel 2 (Klassiker): Restklassen. Dabei ist R⊂ℕ ×ℕ mit R= {< x,y >|xmodn= y modn} für ein festes n.

x modn ist dabei der Rest bei der ganzzahligen Division von x durch n. Beispielsweise ist 7mod2 = 1, weil 5 = 2 × 3 + 1.

Die Äquivalenzklassen für n= 3 wären damit:

Toll daran ist beispielsweise, dass die Menge der Äquivalenzklassen mit der gewohnten Addition und Multiplikation der natürlichen Zahlen genau dann Körper bilden, wenn n prim ist (aber das führt hier zu weit).

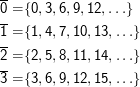
Hüllen

Die reflexive Hülle R^refl einer Relation R entsteht, indem man zu jedem < α,β >∈R noch < α,α > und < β,β > zu R hinzufügt:

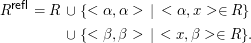
Beispiele: Die reflexive Hülle von < ist ≤. Die reflexive Hülle von ≤ ist ≤ selbst (das gilt natürlich generell: die reflexive Hülle einer reflexiven Relation ist die Relation selbst). Die reflexive Hülle der Relation “x liebt y” führt zu einer Population von NarzistInnen.

Die transitive Hülle R⁺ einer Relation R entsteht, indem man für alle Paare von Tupeln < α,β > und < β, γ > auch das Tupel < α,γ > zu R hinzufügt und das so lange macht, bis sich an R nichts mehr ändert:

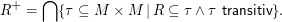
In der formalen Definition werden alle transitiven Relationen über M genommen und diejenigen, die R enthalten, geschnitten. Im Effekt ergibt sich die kleinste transitive Relation, die R enthält (weil diese Teilmenge aller anderen ist und der Schnitt einer Menge mit ihrer Obermenge die Menge selbst liefert) – eben die transitive Hülle.

Da in dieser Vorschrift letzlich über eine Potenzmenge iteriert wird, liefert sie sicher keinen guten Algorithmus zur Berechnung der Hülle. Der würde sich eher aus einer Formalisierung unserer intuitiven Definition ergeben.

Beispiele: Sei R= {< x,y >|y= x+ 1 ∧x,y∈ℕ} die Nachfolgerelation auf den natürlichen Zahlen. Dann ist R⁺ die Größer-Relation auf ℕ.

Die transitive Hülle der Relation “x kennt y” verbindet (vermutlich) alle Menschen auf der Welt direkt.

Die transitive Hülle von “x ist mit y durch eine Straße verbunden” verbindet praktisch alle Orte eines Kontinents oder einer Insel miteinander.

Und noch ein “künstliches” Beispiel, weil die Berechnung der transitiven Hülle manchmal etwas tricky aussieht. Gegeben sei die Relation

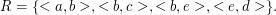
Sie ist offensichtlich nicht transitiv, weil z.B. < a,c > fehlt. Um nun die Hülle zu bauen, sehen wir uns für jedes Tupel das zweite Element an und sehen nach, ob dieses als erstes Element eines Tupels auftaucht. Wenn ja, fügen wir ein neues Paar aus dem ersten Element des Ausgangstupels und dem zweiten Element des gefundenen Tupels hinzu. Das führt im Beispiel zu folgender Relation:

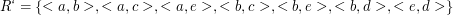
Auch diese Relation ist noch nicht transitiv, weil z.B. < a,d > fehlt. Wir wiederholen die Prozedur:

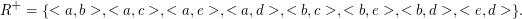
Diese Relation ist transitiv und mithin die transitive Hülle von R.