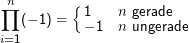Zwei Mengen M1, M2 haben gleiche Kardinalität (sind gleichmächtig) gdw. es eine Bijektion zwischen ihnen gibt.
Insbesondere hat M die Kardinalität n (in Zeichen: |M|= n), wenn es eine Bijektion {1,…,n}→M gibt. Die Menge heißt dann endlich.
Eine Menge, die bijektiv auf die natürlichen Zahlen ℕ abbildbar ist, heißt abzählbar unendlich. Dazu gehören beispielsweise die Brüche. Schreibweise: |M|= ℵ0 (Aleph Null).
Es gibt überabzählbar unendliche Mengen.
Gilt eine Aussage für eine abzählbar unendliche Menge von Objekten, kann ein Induktionsbeweis geführt werden. Dieser besteht aus drei Schritten:
- Induktionsanfang: Behauptung ist für n richtig (meistens n= 0 oder n= 1)
- Induktionsannahme: Die Behauptung gelte für ein beliebiges m≥n
- Induktionsschluss: Aus der Richtigkeit für m folgt die Richtigkeit für m+ 1
Beispiel: ∑ i=0ni= n(n+ 1)∕2.
- Induktionsanfang: n= 1: 0 + 1 = 2∕2
- Induktionsannahme: Behauptung ist für m≥ 1 richtig.
- Induktionsschluss:
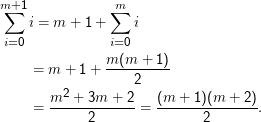
Historische Anmerkung: Das Wort “Induktion” kommt aus der klassischen Logik, wo – grob gesprochen – die Induktion der Schluss vom Speziellen aufs Allgemeine, die Deduktion der Schluss vom Allgemeinen aufs Spezielle ist. An und für sich ist die Induktion ein gefährliches Pflaster, das aus guten Gründen nicht als Beweistechnik zugelassen ist.
Zum Beispiel könnte jemand die speziellen Fälle 1, 3, 5, 7, 11, 13, 17 untersuchen und feststellen, dass alle ungeraden, die er/sie untersucht hat, prim sind. Der Schluss, alle ungeraden Zahlen seien prim, ist natürlich grottenfalsch.
Andererseits hilft die Induktion, die Richtung, in der man suchen soll, zu finden. Im Beispiel könnte man z.B. vermuten, dass alle Primzahlen ungerade sind. Das ist – bis auf den Sonderfall der Zwei – auch richtig, was man dann deduktiv nachweisen kann (im Groben: in allen geraden Zahlen steckt der Primfaktor zwei).
Die vollständige Induktion ist auf der anderen Seite völlig in Ordnung, eben weil sie über abzählbar unendlichen Mengen operiert und auf diese Weise alle Spezialfälle sicher abdecken kann.